Avainsana-arkisto: matematiikka

Kuinka oppia matemaattisen todistamisen taito

10 helmikuun, 2024 paatoimittaja Kommentoi

Kirjoittanut Joseph Mellor

Matemaatikoksi tuleminen tapahtuu kolmen vaiheen kautta: aritmetiikka, algebra ja argumentit (eli todistukset). Useimmat ihmiset oppivat aritmetiikan ja algebran, mutta riippuen urapoluista, he harvoin opettelevat matemaattisen todistamisen taidon. Jopa valinnaisena aiheena opiskeltuna todistukset ovat pelottavia. Opiskelijat käyttävät vuosia oppimaan miten ratkaista ongelmia seuraamalla tiettyjä askelia, ja sitten kaikki tuntuu yhtäkkiä muuttuvan. Derivaatan ketjusäännöillä laskemisen sijaan, nyt täytyykin yhtäkkiä osoittaa, että 2:n neliöjuuri on irrationaalinen. Jos et osaa ratkaisua ulkoa, mistä edes aloittaa?

Tässä artikkelissa haluan antaa joitain ohjeita miten todistaa lauseita matematiikassa samaan tyyliin kuin fysiikan artikkeleissani. Ensimmäinen osio liittyy yleisiin ohjeisiin, keskiosassa käsitellään todistustekniikoita ja loppuosassa puhutaan tempuista, joita voi soveltaa tietynlaisiin ongelmiin. Laitan myös linkkejä oppimateriaaleihin pitääkseni artikkelin lyhyenä ja antaakseni käsityksen useamman tyylisistä todistuksista. Käyn myös perusasiat läpi, mutta voit hyvin hypätä jonkun kohdan yli jos siltä tuntuu.

Kehitä intuitiota ennen siihen luottamista

“Jos ihmiset tietäisivät miten kovasti näin vaivaa päästäkseni tälle tasolle, se ei tuntuisi yhtään hienolta.”
— Michelangelo

Monissa maissa on tietynlaisen “matikkapersoonan” käsite. Jokaisella on oma määritelmänsä “matikkapersoonalle”, mutta yleinen idea on, että jotkut ihmiset ovat syntyneet hyvien matematiikan taitojen kanssa. Sellaisia ihmisiä ei ole oikeasti olemassa. Voi vaikuttaa siltä, että “matikkapersoonat” näkevät ongelman ja tietävät heti miten ratkaista sen, mutta se johtuu vain siitä, että he ovat aiemmin ratkaisseet sen tai ovat nähneet jonkun toisen ratkaisevan senkaltaisia pulmia. Uuden pulman kanssa he käyttävät usein tekniikoita, joita he ovat oppineet, muuntamaan pulman sellaiseen muotoon, että he saavat siitä oivalluksia. Se on heidän intuitionsa. Miten siis voit kehittää intuitiota?

Opiskele todistuksia

Todistuksien katseleminen on helppoa, mutta niiden opiskelu on vaikeampaa. Todistukset usein sivuuttavat sen miten sen keksijä alunperin idean sai päähänsä. Sinulle tämä tarkoittaa, että sinun tulisi kysyä itseltäsi miksi kukaan tekisi asian siten kuin matemaatikko sen teki. Saatat ehkä jopa haluta kokeilla jotain erilaista ja katsoa miksi se ei toimi (jos se toimii, silloin olet keksinyt uuden todistuksen). Vaihtoehtoisesti, yritä etsiä samankaltainen todistus tai todistus samankaltaisesta ongelmasta ja katso onko tuon todistuksen ymmärtäminen avuksi alkuperäisen todistuksen ymmärtämisessä.

Infoaikana hyvien todistusten etsiminen on joko verkkolähteiden etsimistä tai oppikirjojen kahlaamista. Jos et tiedä mistä aloittaa, julkaisin artikkelin, jossa on linkkejä moniin relevantteihin lähteisiin. Linkkaan myös todistuskohtaisia lähteitä tähän artikkeliin. Voit etsiä asiaan vihkiytyneiltä foorumeilta suosituksia kirjoille. Jos olet kiinnostunut tietystä aiheesta, etsi aiheesta kurssi minkä tahansa yliopiston sivulta, tutki esitietovaatimuksia ja etsi niistä kursseja.

Konseptien opiskelu

Todistuksia opiskellessa tulisi opiskella myös eri matematiikan alojen konsepteja. Se antaa paremman ymmärryksen, jota tarvitaan erilaisten todistusten ymmärtämiseksi, ja jokainen opittu konsepti on työkalu työkalupakissa. Jos haluat esimerkiksi todistaa, että Rubikin kuutio on mahdollista ratkaista alle 30 siirrolla, ilman ryhmäteoriaa olet umpikujassa. Lisäksi monet matematiikan osa-alueet ovat päällekkäin toistensa kanssa, jolloin tietoisuuden laajentaminen auttaa monin eri tavoin.

Todista se itse

Viimeisenä, yritä itse todistaa asioita. Tässä kohtaa aiemman otsikon ”ennen siihen luottamista” tulee mukaan kuvioon. Olen nähnyt opiskelijoiden aloittavan oikealla idealla ja hylkäävän sen ennenaikaisesti, koska he eivät usko sen toimivan. Sen sijaan suosittelisin, että jos et usko jonkin idean toimivan, katso miten pitkälle voit idean kanssa mennä. Useimmissa tapauksissa sattuu yksi seuraavista:

Idea toimii ja todistus on valmis.
Idea toimii joissain erikoistapauksissa.
Osoittautuu, ettei idea toimi, mutta se luo perustan paremmalle idealle.
Osoittautuu, ettei idea toimi, mutta sait harjoitusta todistaessasi ettei idea toimi.

Kokemuksen karttuessa sinulla on parempi ymmärrys mitkä ideat toimivat ja haaskaat vähemmän aikaa. Lisäbonuksena nihkeä tunne siitä, että luulet todistaneesi jotain mutta et edelleenkään ole varma onnistuitko, katoaa.

Matematiikan ulkopuolella

Voit soveltaa tässä esitettyä melkein mihin tahansa tehtävään, joka ei vaadi fyysistä voimaa. Todennäköisesti minkä tahansa matematiikkaan liittyvän termin voisi korvata shakkiin liittyvällä termillä ja voisi laittaa Daniel Naroditskyn (shakin mestari ja opettaja Youtubessa ja Twitchissa) videolle siitä puhumaan ja kukaan ei huomaisi mitään eroa.

*kuva: Dan-Cristian Pădureț /* *Unsplash*

Mikä on todistus?

Jotta ymmärtäisi mikä tekee todistuksesta todistuksen, pitää ymmärtää ensin muutama määritelmä.

Mitä on matematiikka?

Matematiikkaa kuvataan yleensä sen osa-alueiden, kuten joukko-opin, algebran, laskennan, funktionaalianalyysin jne., muodostamana kokonaisuutena, mutta tämä määritelmä ei ole hyödyllinen ihmisille, jotka eivät jo ymmärrä muutamia näistä osa-alueista. Sen sijaan haluan määritellä matematiikan joukoksi määritelmiä (eli aksioomia) ja sääntöjä (eli logiikkaa). Siinä kaikki. Saattaa kuulostaa siltä, että vähättelen matematiikkaa, mutta älä pidä yleisyyttä heikkoutena. Kaikki, mikä voidaan kuvata määrittelyjen ja sääntöjen avulla, voidaan kuvata matematiikan tai logiikan avulla.

Mikä on propositio?

Propositio on väittämä, joka voi olla joko tosi tai epätosi. ”Kaksi plus kaksi on neljä.” on tosi väite, ”Kaksi plus kaksi on viisi.” on väärä väite, eikä ”Väritön vihreä nukkuu raivokkaasti.” eikä ”Mikä on aurinko?” ole väite. Monimutkaisempi propositio olisi jotain Heine-Cantorin lauseen kaltaista, jossa sanotaan: ”Jokainen jatkuva funktio kompaktilla välillä on tasaisen jatkuva”.

Mikä on todistus?

Todistus on matemaattisten toteamusten ketju, joka selvittää onko jokin propositio tosi vai epätosi. Nämä matemaattiset toteamukset tulee aloittaa määritelmillä ja niiden tulee seurata logiikan sääntöjä. Yleisesti todistukset näyttävät tältä:

Määritelmän mukaan, voimme todeta A.
Loogisen säännön X mukaan, kun otetaan huomioon A, voimme todeta B.
Loogisen säännön Y mukaan, kun otetaan huomioon B, olemme osoittaneet proposition S epä/todeksi.

Jos pidät matematiikkaa pelinä, jossa on omat säännöt ja pelinappulat (eli siis muodollisuutensa), voit pitää todistusta kuin sarjana siirtoja pelissä.

Mikä on lause?

Lause on todistuksen tulos. Aivan kuten on mahdollista käyttää toisten kirjoittamaa koodia oman kirjaston kirjoittamiseen, voit käyttää toisten työtä todistuksen kirjoittamiseen. Esimerkiksi, voin osoittaa, että x² välillä [0, 1] on tasaisesti jatkuva osoittamalla, että se on jatkuva ja että [0, 1] on suljettu väli. Sitten lainaan Heine-Cantor -lausetta ja olen valmis.

*Digitaalipiirit ovat Boolen algebran fyysisiä toteutuksia. Kuva Samer Khodeir / Unsplash*

Opi formaalin logiikan perusteet

“Sitä paitsi on virhe uskoa, että täsmällisyys on yksinkertaisuuden vihollinen. Päinvastoin, lukuisat esimerkit vahvistavat, että täsmällinen menetelmä on samalla yksinkertaisempi ja helpommin ymmärrettävä. Juuri pyrkimys täsmällisyyteen pakottaa meidät etsimään yksinkertaisempia todistusmenetelmiä.”
— David Hilbert

Saatat lukea tätä kappaletta ja miettiä ”eikö tuo sano samaa kuin artikkelin otsikko”. Ei. Formaali logiikka koostuu joukosta määritelmiä ja sääntöjä, jotka muodostavat useimpien argumenttien pohjan. Tämä osuus tulee olemaan pitkä, mutta käsittelen suurimman osan siitä mitä tietoja tarvitset.

Boolen algebra

Otetaan väittämä ”Jos henkilö kävelee sateessa tai hyppää altaaseen, hän kastuu.” Jättäen huomiotta sadevaatteet ja sateenvarjot, miten voisit esittää, että tämä väittämä on totta? Vaikka me menemme seuraavassa osiossa todistustekniikoihin, nämä tekniikat ovat oikopolkuja totuustauluun, taulukkoon joka ottaa jokaisen mainitun väittämän totuusarvon ja tarkastelee mitä tapahtuu kun niiden totuusarvo on joko totta tai epätotta. Proposition osoittamiseksi me näytämme, että väitteen sarake taulussa on aina totta.

Todistus: Sateessa kävely

Meidän tapauksessamme meillä on kaksi syötelausetta:

Henkilö kävelee sateessa.
Henkilö hyppää altaaseen.

Ja kolme tuloslausetta:

Henkilö kastuu.
(Henkilö kävelee sateessa) TAI (henkilö hyppää altaaseen).
JOS ((henkilö kävelee sateessa) TAI (henkilö hyppää altaaseen)), SILLOIN (henkilö kastuu).

Olen lisännyt sulkeita, jotta voit nähdä miten lauseet rakentuvat yhdistelemällä yksinkertaisempia. Totuustaulun koostamiseksi tarkastelemme mitä tapahtuu, kun me asetamme jokaisen syötelauseen joko todeksi tai epätodeksi ja sitten käytämme formaalilogiikan sääntöjä (eli Boolen algebraa) täyttämään totuustaulun loppuun.

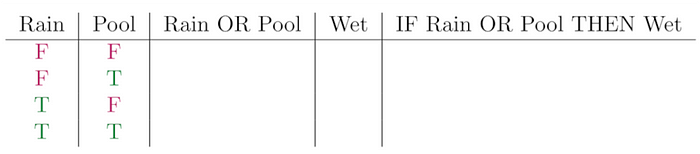
*Voit tarkastaa, että nämä ovat kaikki mahdolliset tapaukset syötelauseille.*

Meidän tulee tietää totuustaulut x TAI y:lle sekä JOS x NIIN y:lle, jotka näkyvät alla.

x TAI y on totta jos x on tosi, y on tosi tai molemmat ovat totta. Väittämässä JOS x NIIN y x:ää kutsutaanedeltäjäksi ja y:ä seuraamukseksi. Me voimme täyttää yhden sarakkeen lisää taulussa.

*Huomaa ensimmäisten kolmen sarakkeen näyttävän tarkalleen samalta kuin ylemmässä totuustaulussa.*

Samoin, JOS x NIIN y on tosi, kun x on epätosi tai molemmat x ja y ovat tosia. Tämä totuustaulu tulisi olla järkeenkäypä: Jos esimerkiksi meillä on väittämä ”jos kävelet sateessa, silloin kastut”; jos olet kävellyt sateessa, niin olet kastunut. Jos et kuitenkaan kävellyt sateessa, silloin meitä ei kiinnosta kastuitko ja näin väittämä on tosi. Jos kävelet sateessa kastumatta, silloin väittämä on epätosi.

Tämän väittämän osoittaminen todeksi tai epätodeksi tarkoittaa, että täytämme JOS x NIIN y:n sarakkeen. Jos kaikki kohdat ovat totta, silloin propositio on tosi. Muutoin se on epätosi. Voimme täyttää yhden solun sarakkeesta heti ilman katsomatta varsinaista todistusta: sen missä x TAI y on epätosi.

JOS x NIIN y on automaattisesti tosi jos x on epätosi. Muissa tapauksissa meidän pitää täyttää sarake. Tämän tekeminen 100-prosenttisen muodollisesti tarkoittaa, että joudumme aloittamaan kaikkien väittämän termien määritelmistä, tai joudumme siteeraamaan jotain lausetta. Esimerkiksi, jos joku osoittaisi että ”jos kävelet sateessa, niin kastut”, me voimme viitata lauseeseen täyttääksemme kohdat sarakkeista jossa (Henkilö kävelee sateessa) on tosi.

*Alimmalla kahdella rivillä (Henkilö kävelee sateessa) on tosi, joten lauseemme tarkoittaa, että alimmat kaksi riviä (Henkilö kastuu) on oltava tosi.*

Mutta sanotaan, että meillä ei ole mitään lausetta väitteelle (henkilö hyppää altaaseen). Silloin meidän on mentävä märän määritelmään, joka on “peitetty tai liotettu vedellä”. Me voimme sitten vedota veden ominaisuuksiin, ihmisen ihon ominaisuuksiin ja altaan määritelmään väittääksemme, että jos hyppäät altaaseen, vesi koskettaa kehoasi ja peityt siihen ja sen tähden kastut. Me voimme sitten käyttää tätä määritelmää täyttämään loput kohdat y-sarakkeesta.

Toinen ja neljäs rivi (henkilö hyppää altaaseen) ovat tosia, joten todistuksemme tarkoittaa, että toisen ja neljännen rivin on oltava tosi. Me tavallaan täytimme neljännen rivin kahdesti, mutta se ei haittaa.

Voimme täyttää taulusta loput katsomalla totuustaulua kohdasta JOS x NIIN y, ja päätyä tosiarvoon, joten todistus on valmis.

Täytämme loput kolme riviä arvolla tosi, koska viimeisellä kolmella riviä ovat (Sataa TAI allas) ja (Kastuu) tosia, mikä vastaa neljännen rivin totuustaulua JOS x NIIN y.

Totuustaulumenetelmä on kaikkien muiden menetelmien selkäranka, mutta sitä harvoin käytetään tässä muodossa, koska se on aika työläs. Jos mahdollista, sinun kannattaa yrittää nähdä miten muut menetelmät liittyvät tähän.

Muita Boolen algebraan liittyviä asioita

Boolen algebrassa on pari muutakin operaatiota, mutta keskeisimmät ovat EI sekä JA, joiden totuustaulut ovat seuraavat.

Pelkillä TAI, EI sekä JA, on mahdollista rakentaa kaikki muut loogiset operaatiot, myös JOS x NIIN y. Voit rakentaa ne kaikki invertoidulla JA-operaatiolla (NAND), joka yhdistää EI ja JA -operaatiot, tai invertoidulla TAI-operaatiolla, eli NOR, joka yhdistää EI sekä TAI -operaatiot, mutta sähköinsinöörit murehtivat näitä sitten enemmän.

Kvanttorit ja joukko-opin perusteita

Jos mietit joukkoa listana asioita, jossa yhtäkään asiaa ei toisteta, se riittää useimmassa tapauksessa. Matematiikassa on kolme kvanttoria:

Eksistentiaalikvanttori: Tämä kvanttori sanoo, että joukolla on alkio. Se luetaan “joukossa on olemassa alkio”. Matematiikassa kirjoitamme sen merkillä ∃. Esimerkki kvanttorin käytöstä olisi “on olemassa luonnollinen luku (1, 2, 3,…) joka on jaolla luvulla kolme, joka on sen monikerta” (esim. 6, 9, 12, …).
Yksikäsitteisyyskvanttori: Tämä kvanttori sanoo, että joukossa on tasan yksi alkio. Matematiikassa se kirjoitetaan ∃!. Se luetaan “on olemassa tasan yksi luonnollinen luku, joka on jaollinen luvulla 3 ja joka on alkuluku” (eli 3).
Universaalikvanttori: Tämä kvanttori sanoo, että kaikilla joukon alkioilla on tietty ominaisuus. Se luetaan “jokaiselle alkiolle joukossa”. Matematiikassa se kirjoitetaan merkillä ∀. Esimerkki kvanttorista olisi “jokaisella luonnollisella luvulla on olemassa sitä suurempi luonnollinen luku” (luvulle 7 voimme nimetä 8, 9, 10, 100 tai 10¹⁰⁰⁰⁰ esimerkkeinä).

Propositiot matematiikassa

Kuten näit universaalikvanttorin esimerkissä, voimme yhdistää kvanttoreita muodostamaan formaaleja propositioita. Normaalisti määrittelemme näiden propositioiden muuttujat niin, että voimme käyttää niitä myöhemmin. Esimerkiksi, voimme lausua universaalikvanttorin esimerkin “jokaiselle x luonnollisissa luvuissa on olemassa y luonnollisissa luvuissa niin, että y on suurempi kuin x”. Matemaattisesti kirjoittaisimme

Tämän proposition todistamiseksi me kuljemme vasemmalta oikealle. Ensimmäinen termi on ”jokaiselle x”, eli x on syötemuuttuja todistuksessamme. ∈ tarkoittaa, että x tulee kuulua sen jälkeen tulevaan joukkoon, joka on ℕ, luonnolliset luvut. Toinen termi on “on olemassa y”, joten meidän tulee osoittaa, että on olemassa y joka toteuttaa proposition lopun. Viimeisenä meillä on y > x, joka on proposition loppuosa.

Päättelysäännöt

On olemassa monia eri päättelysääntöjä joita voit käyttää, mutta tulet käyttämään niitä jokatapauksessa vaikka et edes niistä tietäisi. Me käytimme disjunktion eliminointia päättelysääntönä todistuksessamme. Haluan kuitenkin näyttää muutaman kvanttoreihin liittyvän päättelysäännön.

Universaali Instansiaatio: Jos kaikilla joukon alkioilla on jokin ominaisuus, ja x on joukon alkio, silloin x:llä on tuo ominaisuus. Esimerkiksi, kaikki ihmiset ovat kuolevaisia. Sokrates on ihminen. Niinpä Sokrates on kuolevainen. Tätä temppua voi käyttää osoittamalla, että jokin objekti kuuluu johonkin ominaisuuksien joukkoon, kun haluat objektilla olevan jonkin ominaisuuden.
Eksistentiaalinen Yleistys: Jos objektilla on jokin ominaisuus, silloin on olemassa objekti, jolla on tuo ominaisuus. Esimerkiksi, minulla on tietokone, siispä on olemassa joku jolla on tietokone. Tätä temppua voi käyttää aina kun tietää konkreettisen esimerkin.
Eksistentiaalinen Instansiaatio: Jos on olemassa jjokin objekti jollain ominaisuudella, silloin voit antaa nimen tuolle elementille ja käyttää sitä todistuksen loppuajan. Esimerkiksi, jos sanon todistavani, että on olemassa jokin luku, joka on jonkin yhtälön ratkaisu, voin antaa sille nimen ja käyttää sitä lopun todistuksen ajan sanomalla “olkoon k tämän yhtälön ratkaisu”.

Nämä ovat teknisiä juttuja, joita en aktiivisesti ajattele edes käyttäväni, mutta on avuksi tietää että ne ovat olemassa.

Tunne keskeiset todistusmenetelmät

Nyt voimme alkaa käsitellä todistuksia. Tässä osiossa käsittelemme keskeisiä todistustyyppejä ja annamme joitain ehdotuksia milloin käyttää niitä. Ohjelmoijat voivat pitää näitä menetelmiä eräänlaisena viitekehyksenä. Ne antavat jonkinlaista rakennetta, ja sitten voit itse täyttää loput yksityiskohdat.

Suora todistus

Palatkaamme takaisin todistukseen, jonka teimme totuustauluilla. Me emme koskaan täyttäneet ensimmäistä riviä (henkilö kastuu) koska meitä ei kiinnostanut se tapaus jossa henkilö ei kävellyt sateessa tai ei hypännyt altaaseen. Toisin sanoen, me tarkastelimme ainoastaan tapauksia, joissa x on tosi todistuksessamme. Sellainen todistus tunnetaan nimellä suora todistus. Yleiset askeleet suoraassa todistuksessa ovat

Oleta, että x on tosi.
Käytä sitä seikkaa, että x on tosi, näyttämään, että myös y:n on oltava tosi.

Me oletimme, että henkilö käveli sateessa tai hyppäsi altaaseen, ja sitten näytimme, että vesi oli koskettanut henkilön ihoa ja se kasteli hänet (minun olisi pitänyt valita esimerkki, missä ei käytetä ilmaisuja “henkilön iho” ja “kastua”.). Koska me tarkastelimme kaikkia tapauksia erikseen, todistus tunnetaan nimellä kaikkien tapausten läpikäynti.

Todistus: Ei ole olemassa suurinta mahdollista luonnollista lukua

Propositiona on “kaikille luonnollisille luvuille on olemassa suurempi luonnollinen luku”. Helpoin tapa todistaa tämä propositio on keksiä joukko askelia, jossa otetaan luonnollinen luku ja sitten tuotetaan suurempi luonnollinen luku. Voimme tehdä sellaisen joko lisäämällä luvun yksi tai kertomalla luvulla kaksi (en laske nollaa luonnolliseksi luvuksi.).

*Oikealla lukee mitä päättelysääntöä ollaan käytetty.*

Tämänkaltainen todistus tunnetaan nimellä rakenteinen todistus, sillä me olemme keksineet keinon rakentaa esimerkin, jolla propositio pätee jokaisella luonnollisella luvulla.

Ääretön totuustaulukko?

Huomaat, että totuustaulu yllä esitetylle todistukselle olisi joutunut olemaan ääretön. Me tarvitsemme yhden rivin jokaista mahdollista luonnollista lukua varten, mikä on ongelma koska emme voi tarkastaa onko jokainen rivi totta. Onneksi voimme päästä pois tästä ongelmasta, koska meidän tarvitsee tarkistaa vain, että se pätee jokaiselle käyttämällemme luonnolliselle luvulle. Tavallaan todistuksemme on enemmänkin pohja jolla osoittaa proposition olevan totta aina sille tietylle tapaukselle, jonka parissa työskentelemme.

Tunnetumpi esimerkki on differentiaalilaskennan/reaalianalyysin raja-arvot, jotka perustuvat siihen miten lähelle haluat päästä vastausta. Esimerkiksi, jos meillä on vaikka raja-arvo

f(n) perustuu arctan(x):n Taylorin sarjaan, ja käytän John Machinin kaavaa laskemaan π:n.

Muodollisesti meillä on

x ⇒ y on silloin sama kuin JOS x NIIN y.

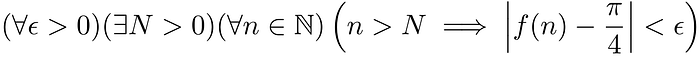
Yksinkertaisimmin ilmaistuna, tämä kaava sanoo, että me voimme päästä niin lähelle kuin haluamme arvoa π/4 (ϵ on se luku miten lähelle haluamme päästä vastausta) summaamalla äärellisen määrän termejä (N on termien minimilukumäärä). Sanokaamme, että haluamme laskea ensimmäiset 100 desimaalia luvusta π/4. Siinä tapauksessa, meitä kiinnostaa ainoastaan ϵ = 1/10¹⁰⁰ ja niinpä totuustaulussamme olisi vain yksi rivi. Me voimme sitten sijoittaa tuon arvon ϵ määrittääksemme raja-arvon avulla N ≈ 69.

Todistus: Pythagoraan lause

Pythagoraan lauseella on tässä vaiheessa yli 100 todistusta, mutta näytän suosikkini. Tämän todistuksen ymmärtämiseksi ainoa mitä pitää tietää on

kolmion kulmien summa on 180 astetta,
suorien kulmien suuruus on 90 astetta,
nelikulmion pinta-ala lasketaan kanta kertaa korkeus,
ja kolmion pinta-ala on kanta kertaa korkeus jaettuna kahdella.

Huomaa, että kun on tiedossa neliöiden sivut ja suora kulma, pinta-alan laskeminen on varsin luonnollista.

Ainoa mitä tehdään on järjestellään kolmiot muodostamaan neliö (jonka voit tehdä ensimmäisen ja viimeisen faktan perusteella), sitten lasketaan pinkin neliön pinta-ala kahdella tavalla:

Koska se on neliö, voit laskea sen pinta-alan neliöimällä sivun pituus: c².
Vaihtoehtoisesti voit laskea suuren neliön pinta-alan (Suuri neliö: (a + b)² = a² + 2ab + b²) ja sitten vähentää kolmioiden pinta-alat (Yksi kolmio: ab/2, neljä kolmiota: 4 (ab/2) = 2ab). Jos teet niin, tulee tulokseksi a² + 2ab + b² – 2ab = a² + b².

Koska molemmat kaavat kuvaavat samaa pinta-alaa, niiden on oltava yhtäsuuret, mikä tarkoittaa a² + b² = c², ja Pythagoraan lause on todistettu.

Kontrapositiiviset todistukset

Koska meillä on suoria todistuksia, voitaisiin myös spekuloida, että on olemassa epäsuoria todistuksia. Se pitää paikkansa. Epäsuoran todistuksen ymmärtämiseksi tarkastellaan totuustaulua JOS x NIIN y.

Ainoa tapa, jolla propositio olisi epätosi, on jos x on tosi, mutta y epätosi. Proposition osoittaminen todeksi on mahdollista osoittamalla, että me emme koskaan saavuta tapausta, jolloin x on tosi mutta y epätosi olettamalla, että y on epätosi ja näyttämällä että x ei voi olla tosi. Tämän kaltainen epäsuora todistus tunnetaan nimellä kontrapositiivinen todistus. Latinaksi sen nimi on modus tollens.

Todistus: Neliöt ja parilliset luvut

Esimerkiksi, tarkastellaan väittämää “jos n² on pariton, silloin n on parillinen”. Suora todistus toimisi tässä, kun vetoamme aritmetiikan peruslauseeseen, mutta pidän kontrapositiota yksinkertaisempana. Tässä tapauksessa haluamme näyttää, että “jos n on pariton, silloin n² on pariton”. Koska meillä ei ole parempaakaan tekemistä, tarkastellaan määritelmiä. Jos me tarkastelemme parittoman luvun määritelmää, huomaamme että luonnollinen luku x on pariton jos ja vain jos on olemassa luonnollinen luku k siten että 2 k – 1 = x. Koska n on pariton oletuksemme perusteella, asetamme m sellaiseksi luvuksi, että 2 m – 1 = n Eksistentiaalisen Instansiaation avulla. Sitten voimme sijoittaa 2 m – 1 lausekkeeseen n² ja algebran avulla saada 4 m² – 4 m+ 1. Tämä voidaan ottaa tekijöiksi 2 ( 2 m² – 2 m ) + 1 tai 2 ( 2 m² – 2 m + 1) – 1. Tästä lausekkeesta voimme todeta, että n² on pariton, koska me voimme asettaa k siten, että 2 k – 1 = n², eli siis k = 2 m² – 2 m + 1.

Kontrapositiivisen todistuksen ensimmäisen askeleen jälkeen loput todistuksesta voi olla mitä tahansa. Todistus yllä on suora todistus sille, että “jos n on pariton, niin n² on pariton”.

Todistus vastaväittämällä

Todistus vastaväittämällä on toisenlainen epäsuora todistus. Se eroaa muunlaisista todistuksista, sillä se nojaa rajoitukseen, että loogisten järjestelmien tulee olla myös johdonmukaisia ollakseen hyödyllisiä. Yleinen vastaväittämällä todistamisen menetelmä on näyttää, että jos väittämä olisi epätosi, siitä seuraa ristiriita.

Todistus vastaväittämällä toimii hyvin kaiken kanssa, mutta haluan keskittyä epärakenteisten todistusten esimerkkiin. Toisin kuten rakenteiset todistukset, epärakenteiset todistukset eivät mahdollista tapaa rakentaa esimerkkejä. Sen sijaan ne käyttävät useita olemassaololauseita kuten kyyhkyslakkaperiaate tai väliarvolause.

Todistus: Irrationaaliluvuissa toistuu ainakin yksi numero äärettömän monta kertaa

Tarkastellaan väittämää “irrationaaliluvun desimaaliesityksessä toistuu ainakin yksi numero äärettömän monta kertaa”. Oletetaan, että mikään numero ei toistu äärettömän monta kertaa irrationaaliluvun desimaaliesityksessä. Siinä tapauksessa kaikkien numeroiden tulee esiintyä äärellisen monta kertaa. Koska meillä on vain kymmenen numeroa, joista jokainen esiintyy äärellisen monta kertaa, numeroiden yhteenlaskettu lukumäärä tulee olla äärellinen. Me kuitenkin tiedämme, että irrationaaliluvuilla on oltava ääretön määrä numeroita. Meillä on ristiriita. Oletuksemme on oltava epätosi, mikä tarkoittaa että väittämämme on tosi, ja todistus on valmis. Koska me emme maininneet mikä tuo numero on, tämä todistus ei voi olla rakenteinen.

Kyyhkyslakkaperiaate

Minun onnistui keksiä todistus käyttämällä kyyhkyslakkaperiaatetta. Jotta sinäkin voisit kokea saman, tässä on seitsemän todistusta, joissa kyyhkyslakkaa on käytetty.

Matemaattinen induktio

Matemaattinen induktio on eräänlainen suora todistus. Siinä näytetään, että propositio on tosi jollekin perustapaukselle, sitten näytetään että perustapaus yhdistettynä propositioon (induktiohypoteesi) tarkoittaa, että propositio pätee kaikissa tapauksissa. Useimpien todistusten kanssa perustapaus on jokin luonnollinen luku k, ja “kaikki tapaukset” viittaavat kaikkiin luonnollisiin lukuihin, jotka ovat suurempia tai yhtä suuria kuin k.

Induktiota usein verrataan dominoihin, induktioaskel on kuin jokaisen dominopalikan pystytys ja perustapaus on ensimmäisen dominon kaataminen.

Todistus: Ensimmäisen N parittoman luvun summa

Induktio toimii hyvin pulmiin, joihin liittyy summaamista, seuraavakaan ei ole mikään poikkeus. Me voimme esittää ensimmäisen N parittoman luvun summan

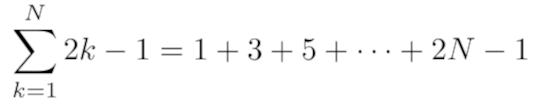
Niille jotka tuntevat ohjelmointia, tämä muoto voidaan esittää for -silmukoina.

Jos et jo tunne kaavaa, kannattaa ensin tarkastella muutamaa ensimmäistä termiä.

Nämä näyttävät ensimmäisiltä lukujen neliöiltä. Esitämme konjektuurin (matematiikan kielellä “arvaus”) että ensimmäisten N parittoman luvun summa on N². Nyt todistamme sen. Me olemme jo osoittaneet perustapauksen pätevän, sillä 1 = 1². Seuraavaksi tarkastelemme induktioaskelta. Oletamme, että olemme osoittaneet ensimmäiset N tai N – 1 lukua. Tässä tapauksessa sanon N – 1 (kumpikin toimii, joten voit heittää vaikka kolikkoa jos et osaa valita), joka tarkoittaa

Me joudumme käyttämään tätä tulosta soveltaaksemme sitä luvun N – 1 jälkeen tulevaan lukuun, joka on N. Jos olisimme valinneet N, silloin käsittelisimme tapausta N + 1. Juuri nyt meillä on kaksi tapaa laskea summa:

Sijoita N kaavaan ja laske N².
Lisää seuraava termi (2 N +1) summaan.

Molemmissa tapauksissa pitäisi saada N². Tässä kohtaa algebran avulla käytämme induktiohypoteesia.

Ensimmäiset kaksi riviä ovat ensimmäinen tapa laskea summa ja loput rivit ovat toinen tapa.

Tämä todistus käytti heikon induktion menetelmää, koska me oletimme proposition pätevän vain lukuun N – 1 asti. Vahvassa induktiossa oletetaan, että propositio pätee kaikille arvoille alle N. Vahva induktio on yhtä hyvä kuin heikko induktio, vahvalla induktiolla on vain vahvempi induktio-oletus.

Todistus: Aritmetiikan peruslause (vahva induktio)

Aritmetiikan peruslause sanoo, että jokainen ykköstä suurempi luonnollinen luku on hajoitettavissa alkulukutekijöihin. Esimerkiksi luku 12 voidaan kirjoittaa 2² × 3, kun taas 17 voidaan kirjoittaa 17. Tässä on todistus sille, että voit hajoittaa jokaisen luvun alkulukutekijöihinsä.

Yksikäsitteisyyden todistaminen vaatii tietoa jakosäännöistä, joita en ole käsitellyt.

Joukkoonkuuluvuusperiaate

Joillekin propositioille induktiotodistus on liian hankalaa, mutta se saattaa silti toimia. Vaihtoehtona voimme käyttää joukkoonkuuluvuusperiaatetta. Sen mukaan jokaisella luonnollisten lukujen osajoukolla on ainakin yksi alkio. Kun käytämme joukkoonkuuluvusperiaatetta todistuksessa vastaväittämän avulla, aloitamme olettamalla, että on olemassa luonnollisten lukujen ei-tyhjä joukko, jolle todistettava propositio ei päde. Kutsumme tätä epätodeksi joukoksi. Sitten sovellamme joukkoonkuuluvuusperiaatetta valitsemaan kyseisen joukon pienimmän alkion. Sitten käytämme tuota alkiota osoittamaan ristiriidan. Yleensä osoitetaan jompi kumpi:

että väittämä on tosi epätoden joukon pienimmälle alkiolle, tai
että epätoden joukon pienin alkio ei ole joukon pienin alkio.

Kummassakin tapauksessa ainoa tapa välttää ristiriitaa on, että epätosi joukko on tyhjä.

Todistus: Aritmetiikan peruslause

Vaikka olemmekin jo todistaneet tämän, on hyvä esittää vaihtoehtoinen todistus. Tässä todistuksessa näytämme, että propositio pätee epätoden joukon pienimmälle alkiolle.

Tämän todistuksen ensimmäinen osa tulisi näyttää varsin samanlaiselta kuin vahvalla induktiolla todistaminen.

Todistus: kahden neliöjuuren irrationaalisuus

Tässä tapauksessa käytämme tietyn tyyppistä todistusta, joka perustuu joukkoonkuuluvuusperiaatteeseen, nimeltään äärettömän laskeutumisen menetelmä. Äärettömän laskeutumisen menetelmässä oletetaan, että ollaan löydetty joukon pienin alkio tietylle luonnollisten lukujen joukolle, ja sitten käytetään tuota alkiota tuottamaan pienempi luonnollinen luku. Sitä kutsutaan äärettömäksi laskeutumiseksi, koska todistusta voi käyttää uudelleen äärettömän monta kertaa tuottamaan vieläkin pienempiä lukuja.

Aivan kuten aiemminkin, olisimme voineet kirjoittaa tämän todistuksen induktiolla, jossa jokainen askel antaa seuraavan osoittajan ja nimittäjän.

Milloin käyttää mitäkin todistusmenetelmää

Jos voisin antaa absoluuttisen vastauksen siihen milloin kutakin todistusmenetelmää voisi käyttää, olisin jo voittanut Fieldsin mitalin. Voin kuitenkin joitain vinkkejä antaa:

Todistus ristiriidalla: tämä on aina mahdollisuus.
Todistus vastaväittämällä: Jos todistettavan asian seurauksen kanssa on helpompaa työskennellä kuin sitä edeltävien oletusten, silloin kannattaa kokeilla vastaväittämää.
Suora todistus: Suorat todistukset ovat hyviä propositioiden kanssa, jotka ovat muotoa “on olemassa x kuuluu A:han siten, että P”, jossa P on jotain mitä voi manipuloida algebralla tai muilla työkaluilla.
Epäsuorat todistukset: Epäsuorat todistukset ovat hyviä propositioihin, jotka ovat muotoa “on olemassa x kuuluu A:han siten, että P”, jossa P nojaa johonkin olemassaololauseeseen, kuten kyyhkyslakkaperiaate, väliarvolause tms.
Induktiotodistus: Induktio on hyvä aina kun voi löytää pienemmän version pulmasta todistettavan pulman sisällä. Esimerrkiksi, ensimmäisten n luvun neliön summa voidaan kirjoittaa ensimmäisten n – 1 neliön summana plus n:s neliö, joten induktio toimii.
Todistus joukkoonkuuluvuusperiaatteella: Joukkoonkuuluvuusperiaate toimii aina kun työskentelee kokonaislukujen tai rationaalilukujen parissa, ja haluaa osoittaa ristiriidan.
Kaikkien tapausten läpikäynti: Suosittelen kaikkien tapausten läpikäyntiä vain, kun tapausten lukumäärä on pieni, tai viimeisenä oljenkortena.

Muuta pulmaa

Nyt kun olemme listanneet yleisimmät todistusmenetelmät, puhutaan hieman muutamista tempuista. Jos jää jumiin johonkin tiettyyn pulmaan, voit koittaa

esittää heikomman väittämän (esim. jos pitää osoittaa, että kaikkien ei-täydellisten lukujen neliöjuuret ovat irrationaalisia, voit osoittaa, että kaikkien alkulukujen neliöjuuret ovat irrationaalisia),
esittää yleisemmän väittämän (esim. triomino-peli, jossa osoitetaan että voi laittaa tyhjän neliön mihin tahansa yhden ainoan paikan sijaan),
tai osoittaa jonkin asiaan liittyvän tai vastakkaisen väittämän (esim. jos halusit osoittaa, että “jos n² on parillinen, silloin n on parillinen”, voit koittaa osoittaa “jos n on parillinen, silloin n² on parillinen” saadaksesi idean siitä mitä sinun tulee tehdä).

Usein ongelman muuttaminen antaa idean siitä minne pitää mennä seuraavaksi. Heikomman väittämän todistuksessa löytää usein todistuksen, joka hajoaa kun alkuperäistä väitettä soveltaa. Siinä kohtaa voi joko yrittää paikata todistusta ja käsitellä erikoistapausta tai keksiä uuden todistuksen, joka täysin välttää hajoamisen. Toisaalta, vahvemman väittämän todistaminen usein siivoaa pois irrelevanttia informaatiota, joka liittyy heikompaan väittämään. Viimeisenä asiaan liittyvän käänteisen väittämän todistaminen voi auttaa ymmärtämään sitä mitä pitää todistaa.

Etsi invariantteja ominaisuuksia

Joskus joutuu käsittelemään pulmia, jotka saattavat vaatia suuremman, mahdollisesti äärettömän, avaruuden tutkimista. Monen tällaisen ongelman tapauksessa voi etsiä ominaisuutta, joka sopii kaikkialle. Me nimitämme sellaista ominaisuutta invariantiksi. Useimmissa tapauksissa nämä invariantit voidaan kirjoittaa jonkinlaisen funktion muotoon, jossa tietyt koordinaatit ovat vakioita. Esimerkiksi, eräs tällainen invariantti on Eulerin karakteristika χ:

Voit soveltaa tätä invarianttia ja vastaavia osoittamaan, että et voi ratkaista ongelmaa pallopinnalla tai tasopinnalla, mutta voit kylläkin toruspinnalla.

Eräs nimekkäimmistä esimerkeistä tulee vuoden 2011 matematiikkaolympalaisista:

563 opiskelijasta ainoastaan 20 sai tämän kysymyksen oikein. Jos kykenet löytämään jonkin invariantin, tämä ongelma muuttuu triviaaliksi. Voit laittaa videon paussille sen jälkeen kun näet kolmioita ja yrittää katsoa osaatko ratkaista ongelman.

Todistus: Conwayn sotilaat

Tämän koko pulman ja sen ratkaisun selittämiseen tarvitaan kokonainen toinen artikkeli. Sen sijaan linkkaan kaksi videota: yksi selittää pelin ja toinen sen todistuksen.

Yllä on pelin selitys.

Alla on todistus.

Liitän mukaan todistuksen esimerkkinä, koska se on varsin helppo seurata, haluan jakaa lisäresursseja todistuksista, haluan antaa tiettyjä esimerkkejä siitä miten antaa numeroita pulmille, joilla ei vaikuta olevan numeroita, joiden perusteella tuottaa invariantteja.

Todistus: Punaiset, valkoiset ja vihreät pallot

Olkoon sinulla 2000 vihreää palloa. Voit tehdä palloilla seuraavaa:

Vaihtaa kaksi punaista palloa yhteen vihreään palloon tai päinvastoin.
Vaihtaa kaksi valkoista palloa vihreään palloon tai päinvastoin.
Vaihtaa kaksi vihreää palloa punaiseen palloon ja valkoiseen palloon tai päinvastoin.

Nyt esitän kaksi kysymystä:

Onko mahdollista olla 1003 punaista palloa äärellisen määrän yllä esitettyjä vaihtoja jälkeen?
Mikä on minimimäärä palloja, joita voi olla?

En anna vastausta tähän, mutta annan yhden vihjeen: yritä antaa palloille numeroita niin, että vaihdot ovat järkeviä. Siitä eteenpäin voit yrittää etsiä invarianttia, joka auttaa vastaamaan kysymykseen. Minua kiinnostaa nähdä miten ihmiset yrittävät ratkaista tämän ongelman.

Käytä tunnettuja temppuja

Vaikka yllä esitetyt menetelmät tulevatkin esiin matematiikan kaikilla osa-alueilla, jotkut alueet käyttävät joitain todistuksia enemmän kuin toiset. Reaalianalyysissa käytetään paljon aikaa tiettyjen ominaisuuksien raja-arvojen etsimiseen, joten käytetään usein temppuja kuten nollan summaaminen kolmioepäyhtälöön tai kaikki tässä Terrence Taon artikkelissa esitetyt temput. Modernissa algebrassa halutaan usein osoittaa, että jokin struktuuri liittyy siihen struktuuriin minkä kanssa halutaan työskennellä. Graafiteoriassa halutaan tarkastella aligraafeja. Paljon pidempi lista löytyy sivulta tricki.org, vaikka sivu vaikuttaakin epäaktiiviselta.

Satunnaisia vinkkejä

Tässä osiossa on joitain vinkkejä, joille ei kannata välttämättä kirjoittaa kokonaista omaa osiotaan:

Jos et tiedä mistä aloittaa, kirjoita ylös kaikki määritelmät tai lauseet, jotka mielestäsi ovat relevantteja.
Mitä enemmän vaivaa näet alussa, sitä enemmän voit antaa matematiikan mennä omaa reittiään.
Työskentele vain parin yksittäistapauksen parissa. Esimerkiksi, yritä työskennellä nollan tai ykkösen kanssa, tai minkä tahansa joka saattaisi olla erikoistapaus.
Jos et osaa keksiä mahdollisia erikoistapauksia, käy läpi useampi tapaus ja katso löydätkö jonkun kaavan.
Usean muuttujan ongelmissa määrittele yksi muuttuja toisten muuttujien avulla. Esimerkiksi jos pulmassa on A ja B, kokeile määritellä B = A + k tai B = c A.
Lisää nolla tai kerro ykkösellä ja kirjoita lauseke eri muotoon niin, että sen kanssa on helpompaa työskennellä.
En piirrä kuvaajia ellen ole geometrian parissa, mutta monet ihmiset suosivat piirtää kuvaajia ymmärtääkseen mistä on kyse.

Tämä artikkeli on jo tarpeeksi pitkä, mutta on paljon enemmänkin eri temppuja kuin mitä listasin.

Lisälukemista

Tämä artikkeli ei todellakaan ole ainoa resurssi matemaattisista todistuksista, joten haluaisin mainita muitakin:

3blue1brownin kanava on hyvä, mutta suosittelisin Lockdown Math -sarjan viimeisintä videota.
Daniel J. Vellemanin How to Prove It: A Structured Approach vaikuttaa olevan standardikirja todistuksille. Melkein kaikki aihepiirit mainitaan ja niitä käsitellään kirjassa, ja siinä on paljon harjoituksia.
Tässä on pruju joka käsittelee sitä jos sattuu jäämään jumiin todistuksissa.
Minun juttusarjani raja-arvoista näyttää muutaman erilaisen todistuksen, mutta käsittelee myös reaalianalyysia.
Tämän videon ja tämän videon kanavat käsittelevät omilla videoillaan todistuksia.
Michael Pennilla on yli tuhat videota eri aiheista.
Terrence Taolla on kirja matikkakilpailutehtävistä varttuneemmille tieteenharjoittajille.

Viimeisenä, artikkelissani Beyond Calculus: The Math Classes You Didn’t Take on paljon resursseja.

Artikkelin julkaissut cantorsparadise.com

Tiede

Johdatus topologiaan

23 tammikuun, 2024 paatoimittaja Kommentoi

Kirjoittanut David S. Richeson

Joustavien muotojen ominaisuuksien väliset suhteet ovat viehättäneet matemaatikoita vuosisatojen ajan.

Jos haluat aloittaa tappelun, kysy yksinkertaisesti ystäviltäsi ”onko Pluto planeetta?” tai ”onko hotdog voileipä?” tai ”kuinka monta reikää on pillissä?”. Ensimmäiseen kahteen kysymykseen vastataan yleensä kyllä tai ei, kolmanteen vastataan kaksi, yksi tai jopa nolla.

Nämä kysymykset riippuvat määritelmistä. Mikä tarkalleen onkaan planeetan määritelmä? Voileivän? Reiän? Me jätämme nämä kaksi ensimmäistä määritelmää kavereillesi. Kolmatta voidaan tarkastella matematiikan linssin läpi. Miten matemaatikot — erityisesti topologit, jotka tutkivat spatiaalisia suhteita — ajattelevat näistä rei’istä?

Illustration showing a human figure sitting on a large straw, gazing at different topological figures.

Arkipäivän kielessä ”reikä” tarkoittaa montaa eri asiaa. Yksi on ontelo, niinkuin maahan kaivettu kuoppa. Toinen on avauma jossain kappaleessa, kuin tunneli vuoren läpi tai selkäpuolelta kierteellä yhteen nidotun päiväkirjan sivuihin puhkomat reiät. Eräs toinen on täysin suljettu tila, kuten emmentaalijuustoon syntyvä ilmakupla. Mutta sen ymmärtämiseksi miksi — ja miksi matemaatikoita edes kiinnostaa reiät — me joudumme matkaamaan topologian historiaan, mikä alkaa siitä miten tämä ala eroaa sen sisaresta, geometriasta.

Geometriassa muodot kuten ympyrät ja monikulmiot ovat kiinteitä kappaleita; niitä analysoidaan pituuksien, kulmien ja pinta-alojen avulla. Mutta topologiassa muodot ovat joustavia, niinkuin kumista tehtyjä. Topologi on vapaa venyttämään ja taivuttelemaan muotoa. Jopa leikkaaminen ja liimaaminen on sallittua, niin kauan kunnes leikkaus liimataan tarkasti. Pallo ja kuutio ovat toisistaan eroteltavia kappaleita, mutta topologille niitä ei voi erottaa toisistaan. Jos haluat matemaattisen oikeutuksen sille, että T-paita ja housut eroavat toisistaan, sinun kannattaa kääntyä topologin puoleen, ei geometrikon. Selitys on: niissä on eri määrä reikiä.

Leonhard Euler käynnisti eri muotojen topologian tutkimukset 1700-luvulla. Sitä voisi luulla, että matemaatikot tiesivät jo melkein kaiken monitahokkaista. Mutta vuonna 1750, Euler keksi minun mielestä erään kaikkien aikojen suurimmista teorioista: jos monitahokkaalla on F monikulmaista tahkoa, E särmää ja V kärkeä, silloin V – E + F = 2. Esimerkiksi, jalkapallossa on 20 valkoista kuusikulmiota ja 12 mustaa viisikulmiota, jotka muodostavat pallomaisen 32 tahkon kappaleen, sekä 90 särmää ja 60 kärkeä. Ja niin 60 – 90 + 32 = 2. Tämä perustason havainto liittyy syvällisellä tavalla moniin matematiikan aloihin, ja kuitenkin se on tarpeeksi yksinkertainen, jotta se voitaisiin opettaa lastentarhan lapsille. Mutta se on kiinnostanut Eukleideksen ja Arkimedeen ja Keplerin kaltaisia geometrikoita vuosisatojen ajan, koska sen tulokset eivät riipu geometriasta. Se riippuu ainoastaan muodosta itsestään: se on topologiaa.

Euler implisiittisesti oletti hänen monitahokkaansa olevan konvekseja (kupera), mikä tarkoittaa, että kappaleen sisällä minkä tahansa kahden pisteen välinen suora tulee pysyä monitahokkaan sisällä. Piakkoin tutkijat löysivätkin poikkeuksia Eulerin kaavaan. Esimerkiksi sveitsiläinen matemaatikko Simon Lhuilier tajusi, että jos poraamme reiän monitahokkaaseen tehdäksemme siitä donitsimaisemman, sen topologia muuttuu ja silloin V – E + F = 0.

Konveksi ja epäkonveksi monitahokas, jossa sovelletaan Eulerin ja Lhuilier’n kaavoja. kuva: Samuel Velasco/Quanta Magazine

Kiinnostavaa kyllä, vaikka Euler ja Lhuilier kuvittelivat monitahokkaansa kiinteiksi, Eulerin kaava lasketaan käyttäen ainoastaan kahta nollaulotteista kärkeä, yksiulotteista särmää ja kaksiulotteista tahkoa. Joten Eulerin kaava (V – E + F) itse asiassa on johdettu kaksiulotteisesta tahokkaasta. Nykypäivänä kuvittelemme nämä muodot ontoiksi kuoriksi.

Lisäksi se mikä ainoastaan merkitsee on kappaleen topologia. Jos teemme monitahokkaan savesta, merkkaamme sen särmät terällä, ja möyhennämme sen palloksi, tahkot ja särmät kaareutuvat, mutta lukumäärä ei muutu. Joten mikä tahansa muoto, joka on topologisesti pallo, sen Eulerin luku on 2; donitsin kaltaiselle torukselle se on 0, tasaiselle levylle se on 1; ja niin edelleen. Jokaisella pinnalla on oma Eulerin lukunsa. Tämä topologinen ymmärrys Eulerin kaavasta — jossa pallot ovat kumimaisia eivätkä kiinteitä — esitettiin ensi kerran Johann Listingin tekstissä vuonna 1861. Vaikka tämä onkin nykyään suurelta osin unohdettu, Listing on myös tunnettu Möbiuksen nauhaan liittyvästä kirjoituksistaan neljä vuotta ennen August Möbiusta. Listing tunnetaan myös koko termin topologia keksijänä.

Eulerin luku V – E + F pallolle on 2, donitsille 0, kiekolle 1, ja tuplatorukselle –2.

Samoihin aikoihin Bernhard Riemann tutki pintoja, jotka tulivat esiin hänen kompleksilukujen tutkimuksissaan. Hän huomasi, että yksi tapa laskea reikiä oli tarkastella miten monta kertaa kappale voitaisiin leikata ilman, että se leikataan kahteen eri palaseen. Rajatulle pinnalle, kuten vaikka pillille joka on avoin kahdesta päästä, jokainen leikkaus tulee alkaa ja päättyä reunaan. Joten Riemannin mukaan, koska pilli voidaan leikata vain kerran — päästä päähän — sillä on tarkalleen yksi reikä. Jos pinnalla ei ole rajaa, niinkuin toruksella, ensimmäinen leikkaus tulee alkaa ja päättyä samaan pisteeseen. Ontto torus voidaan leikata kahdella tavalla — yhden kerran putkesta, ja toisen kerran siitä syntyvästä sylinteristä — joten tämän määritelmän mukaan sillä on kaksi reikää.

Pilli voidaan leikata kerran ilman, että se menee palasiksi, ja ontto torus voidaan leikata kahdesti.

Henri Poincaré oli seuraava, ja hän suuresti laajensi topologian tutkimusalaa julkaisemalla uraauurtavan 123-sivuisen artikkelinsa “Analysis Situs” vuonna 1895. Siinä ja sen viidessä jatko-osassa hän istutti useita topologisia siemeniä, jotka kasvoivat, kukkivat ja kantoivat hedelmää vuosikymmeniä sen jälkeen. Huomattava käsite tässä on homologian käsite, jonka Poincaré yleisti Riemannin korkeampien ulottuvuuksien ideoihin. Homologian avulla Poincaré tavoitteli kuvaavansa kaikkea Riemannin yksiulotteisesta ympyräreiästä pillissä kaksiulotteiseen onteloon kuten emmentaalissa, ja siitä vieläkin korkeampiin ulottuvuuksiin. Näiden reikien määrä — yksi jokaiselle ulottuvuudelle — tunnetaan sittemmin Betti-lukujen nimellä Enrico Bettin kunniaksi, Riemannin ystävän joka oli tehnyt samanlaista tutkimusta.

Moderni homologian määritelmä on varsin syvällinen, mutta se karkeasti tarkoittaa jokaisen muodon liittämistä tiettyyn matemaattiseen objektiin. Tästä objektista voimme kerätä yksinkertaisempaa informaatiota muodosta, niinkuin vaikka sen Bettin luvun tai Eulerin luvun.

Jotta saisimme käsityksen siitä mitä homologia ja Bettin luvut ovat, keskittykääme ensimmäiseen ulottuvuuteen. Aloitamme tarkastelemalla silmukoita pinnalla. Säännöt ovat yksinkertaiset: Silmukat voivat liukua pinnalla, ja jopa ylittää toisensa, mutta ne eivät saa poistua pinnalta. Joillain pinnoilla, kuten ympyrämuotoinen levy tai pallopinta, mikä tahansa silmukka voi kutistua yksittäiseksi pisteeksi. Sellaisilla pinnoilla on triviaali homologia. Mutta toisilla pinnoilla, kuten pilli tai torus, on silmukoita, jotka kiertyvät reikiensä ympäri. Näiden homologia on epätriviaali.

Torus näyttää meille miten visualisoida Bettin lukuja. Me voimme tuottaa äärettömän monia epätriviaaleja silmukoita yhdestä, ja ne voivat kiertyä monta kertaa ympäri ennen kuin ne tulevat takaisin lähtöpisteeseensä. Mutta sen sijaan että kehittelisimme kaoottisen sotkun, nämä silmukat tuottavat elegantin matemaattisen rakenteen. Kutsutaan silmukkaa, joka menee keskusreiän läpi ja kerran putken ympäri nimellä “a.” Tämä on nyt meidän perustamme lisäsilmukoille. Koska silmukka voi mennä putken ympäri kerran, kaksi tai kuinka monta kertaa tahansa, ja kiertosuunnalla on väliä, me voime kutsua näitä silmukoita nimillä kuten a, 2a, –a, ja niin edelleen. Jokainen silmukka ei ole a:n monikerta, kuitenkin sellainen silmukka, joka kiertää keskusreiän ympäri putken kehää pitkin, nimitämme nimellä “b.” Tässä kohtaa ei ole enää muita uniikkeja tapoja kulkea pitkin pintaa: mikä tahansa silmukka toruksen pinnalla voidaan muuntaa silmukoiksi a ja b kertomalla niitä joillain kokonaisluvuilla. Se, että on olemassa joitain yksiulotteisia silmukoita, joista kaikki muut voidaan konstruoida, tarkoittaa että toruksen Bettin luku yhdessä dimensiossa on 2, joka on Riemannin leikkausten lukumäärä.

Toruksella on äärettömän monta eri silmukkaa sen pinnalla. Silmukat a, b ja c ovat kaikki erilaisia, mutta c voidaan esittää silmukoiden a ja b unionina.

Jos silmukka c on ekvivalentti silmukoiden a ja b yhdistelmän kanssa, kirjoitamme c = a + b. Tämä lauseke ei ole pelkästään merkintätapa. Tämä lasku on mahdollista tehdä — silmukoiden summaaminen ja erotus. Matematiikan kielellä joukko, joka mahdollistaa summaamisen ja erotuksen, on nimeltään ryhmä. Joten esimerkiksi toruksen yksiulotteinen homologiaryhmä koostuu ilmaisuista kuten 7a + 5b, 2a – 3b ja niin edelleen.

Ryhmän homologiarakenteen löysi 1920-luvulla Emmy Noether, ryhmien ja muiden algebrallisten rakenteiden tutkimuksen pioneeri. Noetherin havainnon myötä matemaatikot osaavat nyt ottaa käyttöön algebran voiman, rakenteen ja lauseet topologian tutkimukseen. Esimerkiksi me voimme sanoa matemaattisella varmuudella, että pilli, T-paita ja housut topologisesti eroavat toisistaan, koska niiden homologiaryhmät ovat erit. Niillä on eri määrä reikiä.

Miten topologit laskevat reikiä? Bettin lukujen avulla. Nollas Betti-luku b₀ on erikoistapaus. Se yksinkertaisesti laskee objektien lukumäärän. Yksittäiselle yhtenäiselle muodolle b₀ = 1. Niinkuin me juuri näimme, ensimmäinen Bettin luku b₁ on ympyrämäisten reikien lukumäärä muodossa — kuten sylinterimäisen pillin reikä ja toruksen kaksi ympyrämäistä suuntaa. Ja Poincaré näytti meille miten homologian saa lasketuksi, ja näin siihen liittyvät Bettin luvut, myös korkeammissa ulottuvuuksissa: toinen Betti-luku b₂ on onteloiden lukumäärä — kuten pallon, toruksen tai emmentaalijuuston sisässä olevat reiät. Yleisesti b_n kertoo n-ulotteisten reikien lukumäärän.

Poincarén homologia sulkee ympyrän ja tuo meidät takaisin Euleriin. Aivan kuten Eulerin luku voidaan laskea kappaleelle särmien, kärkien ja tahkojen avulla, niin on mahdollista laskea se myös Bettin lukujen avulla: b₀– b₁ + b₂. Torus esimerkiksi on yhtenäinen, joten b₀ = 1; sillä on b₁ = 2, kuten olemme nähneet; ja koska sillä on yksi sisäinen ontelo, b₂ = 1. Niinkuin Lhuilier huomasi, toruksen Eulerin luku on 1 – 2 + 1 = 0.

Vaikka matemaatikoilla onkin ollut perustason ymmärrys homologiasta jo melkein vuosisadan ajan, algebrallinen topologia jatkaa aktiivista tutkimusta aiheesta nivoen yhteen algebran ja topologian. Tutkijat ovat myös haarautuneet muihin suuntiin, kehitellen teoriaa ja algoritmeja, joita tarvitaan eri digitaalisesti esitettyjen muotojen homologian laskemiseen, rakentaen työkaluja joilla identifioida suurten datajoukkojen allaoleva muoto (jotka usein ovat korkeampiulotteisemmissa avaruuksissa), ja niin edelleen.

Toiset tutkijat ovat soveltaneet näitä teoreettisia työkaluja reaalimaailmaan. Kuvittele esimerkiksi sirpaleinen kokoelma pieniä, halpoja antureita, jotka havaitsevat jotain — liikkeen, tulipalon, kaasupäästön — jonkin kiinteän toimintasäteen sisällä. Anturit eivät tiedä sijaintiaan, mutta ne tietävät mitkä toiset anturit ovat lähellä. Vuonna 2007 Vin de Silva ja Robert Ghrist osoittivat miten käyttää homologiaa havaitsemaan reikiä anturien peittoalueessa, perustuen tähän karkeaan informaatioon. Tuoreemmassa tutkimuspaperissa Michelle Feng ja Mason Porter käyttivät uutta pysyvän homologian tekniikkaa havaitsemaan poliittisia saarekkeita — maantieteellisiä reikiä vaaliehdokkaan tukijoukoissa, jotka antavat tukensa vastaehdokkaalle — Kaliforniassa vuoden 2016 presidentinvaalien aikaan.

Niinkuin usean puhtaan matematiikan osa-alueen kanssa, joka on saanut alkunsa pelkkänä teoreettisena pohdiskeluna, topologia on osoittanut käyttökelpoisuutensa reaalimaailmassa, eikä ole pelkästään tyytynyt vastaamaan siihen miten monta reikää pillissä on.

Artikkelin julkaissut Quanta Magazine

luentomoniste suomeksi:

https://dokumen.tips/documents/metriset-avaruudet-ja-topologia-jyvskyln-parkkonemettop2018topo2018pdf.html

Tiede

Neperin luvun monet ominaisuudet

6 marraskuun, 2023 paatoimittaja Kommentoi

kirjoittanut James Round

Viime kuussa esitimme kolme pulmaa, jotka vaikuttivat tarpeeksi tavallisilta, mutta niissä oli numeerinen jekku. Pinnan alta löytyi mystinen transsendenttiluku e. Neperin luku e tunnetaan luonnollisen logaritmin pohjalukuna, joka on ääretön ja jaksollinen desimaaliluku, jonka ensimmäiset 15 desimaalia ovat 2.7 1828 1828 45 90 45… . Miksi luku esiintyy pulmissa niin usein?

Ennen kuin yritämme vastata tähän kysymykseen, meidän pitää oppia hieman enemmän Neperin luvun ominaisuuksista. Kuten transsendentaalinen serkkunsa π, e voidaan esittää lukemattomin eri tavoin — äärettömän sarjan summana, äärettömänä tulona, äärettömänä sarjana, säännöllisenä murtolukujonona ja niin edelleen.

Muistan edelleen, kun kuulin ensikerran luvusta. Tutkimme logaritmeja koulussa, ja ihmettelin sen kykyä muuttaa monimutkaiset ongelmat yksinkertaiseksi summaoperaatioksi pelkästään esittämällä kaikki luvut 10:n eksponenttimurtolukuina. Ihmettelin miten murtoluvut ja irrationaaliset eksponentit oikein lasketaan. Se on tottakai helppoa laskea potensseja kuten 10² ja 10³, ja jos vähän pinnistää, niin voi selvittää mitä on 10^2.5 ottamalla 10⁵:sta neliöjuuren. Mutta miten he keksivät kaiken tämän, niinkuin logaritmitaulukko sanoi, että 20 on 10^1.30103? Miten logaritmitaulukko kaikista luvuista oltiin raavittu kasaan tyhkästä? En vain kyennyt käsittämään miten sellainen voitiin tehdä.

Myöhemmin sain kuulla maagisesta kaavasta, jolla tämän voi tehdä. Se antaa vihjeen siitä mistä “luonnollinen” tulee “luonnollisessa logaritmissa”:

e^x = 1 + x/1!+x²/2!+x³/3!+x⁴/4!+x⁵/5!+⋯.

Negatiivisille eksponenteille joka toinen termi on negatiivinen:

e^-x = 1 – x/1!+x²/2!−x³/3!+x⁴/4!−x⁵/5!+⋯.

Nämä kaavat mahdollistavat minkä tahansa potenssin laskemisen mille tahansa reaalieksponentille, kokonaisluvulle tai murtoluvulle negatiivisesta äärettömästä positiiviseen äärettömään millä tahansa tarkkuudella. Se mahdollistaa täydellisen luonnollisten logaritmien taulukkojen laskemisen, ja siitä muiden yleisten logaritmien, tyhjästä.

Kaavan erikoistapaus saadaan, kun x =1, josta saadaan esitys Neperin luvulle:

e = 1 + 1/1!+1/2!+1/3!+1/4!+1/5!+⋯.

Lisäksi e:llä on monia huikeita ominaisuuksia, joista osaa käsitellään ratkaisuissa pulmiimme. Mutta se ominaisuus, joka on koko luvun olemus ja joka tekee siitä niin luonnollisen logaritmeille ja eksponentiaalisen kasvun tai vaimenemisen tilanteille on tämä:

d/dx e^x= e^x.

Tämä sanoo, että e^x:n muutosnopeus on yhtä suuri kuin funktion arvo jokaisessa pisteessä. Kun x on aika, se kertoo kasvunopeuden (tai vaimenemisen negatiiviselle x:lle), joka on yhtä suuri kuin mitä se on tähän asti kerryttänyt. Reaalimaailmassa on monenmoisia ilmiöitä, jotka tekevät juuri tämän aikajaksoille, ja me esitämme ne esimerkkeinä eksponentiaalisesta kasvusta tai vaimenemisesta. Mutta jos ei puhuta hyödystä, Neperin luvulla on esteettisen täydellisyyden ja luonnollisuuden elementti, joka todella aiheuttaa ihastusta. Siinä on mukana jopa moraalinen opetus; pidän sitä Zen-tyyppisenä funktiona, joka kasvaa aina täydellisen tasapainossa, se ei koskaan saavuta enempää tai vähempää kuin mitä se on jo tähän asti kerryttänyt.

Tarkastellaan nyt sitä miten e esiintyy pulmissamme.

Pulma 1: Ositus

Otetaan mikä tahansa luku, esim. 10. Jaetaan se yhtä suuriin osiin, esim. kaksi 5:sta, ja kerrotaan ne toisillaan: 5 × 5 = 25. Me voisimme jakaa luvun 10 kolmella, neljällä, viidellä tai kuudella ja kertoa kaikki ne yhteen samalla tavalla. Katsotaan mitä tulollemme tapahtuu jos me teemme niin:

2 osaa: 5 × 5 = 25
3 osaa: 3.33 × 3.33 × 3.33 = 37.04
4 osaa: 2.5 × 2.5 × 2.5 × 2.5 = 39.06
5 osaa: 2 × 2 × 2 × 2 × 2 = 32
6 osaa: 1.67 × 1.67 × 1.67 × 1.67 × 1.67 × 1.67 = 21.43

Nähdään, että tulo kasvaa, saavuttaa maksimin ja alkaa pienentyä. Tee sama luvuille 20 ja 30. Huomaat, että sama tapahtuu kaikissa tapauksissa. Tämä ei liity jaettaviin lukuihin itseensä, vaan se on Neperin luvun ominaisuus.

a. Kykenetkö selvittämään missä kohtaa tulo on maksimissaan kullakin luvulla, ja miten se liittyy lukuun e.

Vihjeessä 1a tulo saavuttaa maksiminsa, kun jokaisen osan arvo on lähinnä lukua e. Kaksi suurinta tuloa saadaan silloin, kun jaetut osat ovat luvun e molemmilla puolilla. Pienille arkipäivän luvuille, joita me tässä tarkastelemme, suurin arvo saadaan ositukselle, jonka erotus luvusta e on pienin.

b. Luvulle 10, suurin tulo (39.06) on noin 5.5% suurempi kuin seuraavaksi suurin (37.04). Ilman että lasket oikeaa eroa, osaatko arvata mikä 100:aa pienempi luku on pienin prosenttiosuudeltaan suurimman tulon ja sitä seuraavan välillä? Miksi näin pitäisi olla?

Yllä esitetystä on helppoa nähdä, että kaksi tuloa ovat lähinnä toisiaan, kun kahden vierekkäisen luvun arvot ovat melkein yhtä kaukana e:stä, joista yksi on pienempi kuin e ja toinen suurempi. (Tämä pätee jos ja vain jos funktio on symmetrinen e:n ympäristössä, mitä se ei ole, mutta tämä väli on tarpeeksi riittävä, niinkuin Michel Nizette hienosti asian selitti.) Jos alkuperäinen luku on N, tämä tapahtuu kun murtoluvun N/e suhde on lähellä arvoa 0.5 — eli, kun N/e sijaitsee kahden kokonaisluvun puolivälissä. Jos rakennat taulukon N/e:sta N:n arvoilla nollasta 100:n, ja etsit suhdetta, joka on lähinnä arvoa 0.5, löydät vaaditun kokonaisluvun: 53. Jakamalla 53:n e:llä antaa 19.4976 ja ero on 0.0013% tuloille, jossa on 19 ja 20 osaa.

c. Osaatko selittää miksi e synnyttää tämän ilmeisen yksinkertaisen ongelman?

Niinkuin lukijat Lazar Ilic, Ashok Khatri, Alan Olson, Kurt Godel, TG, Atul Kumar ja Michel Nizette ovat selittäneet, vastaukseen liittyy yksinkertaista differentiaalilaskentaa — pitää etsiä funktion maksimi asettamalla sen derivaatta nollaksi. Funktiomme on (n/x)^x, ja jokaisen osituksen arvo on n/x. Funktion logaritmi on x(ln n/x), ja voimme maksimoida sitä alkuperäisen sijaan, joka on hiukan helpompaa. Jos osaat ratkaista tämän käsin, onnittelut! Jos differentiaalilaskenta ei ole sinun juttusi, voit kirjoittaa “d/dx(x ln n/x) = 0″ Wolfram Alphaan. Derivaatta on ln(n/x) = 1, ja ulos tulee ratkaisu x = ne positiivisille n ja x. Näin optimiosituksen arvo on n/x = e. Voila! Näin e tulee esiin ja antaa maksimitulon.

Tämä opettaa meille, että e:llä on optimaalisuuden ominaisuus. Se voi tulla esiin tilanteissa, joihin liittyy maksimin tai minimin etsintää, niinkuin me näemme pulmassa 2. Perusversio tästä ominaisuudesta näkyy, jos lasket funktion x^1/x arvon kaikille positiivisille reaaliluvuille (tämä tunnetaan Steinerin ongelmana). Kaikista äärettömistä reaaliluvuista se x, joka tuottaa suurimman arvon tälle funktiolle, on e. Funktion x^1/x maksimoiminen on sama kuin maksimoitaisiin (ln x)/x, jonka derivatiivi (1−ln x)/x² on nolla, kun ln x = 1, eli x = e.

Pulma 2: Unioni

Kuten lukijat huomauttivat, tämä pulma oli tunnetun sihteeriongelman variaatio.

Perillinen joutuu valitsemaan 10 parasta puolisokandidaattia seuraavin säännöin. Kandidaatteja haastatellaan yksi kerrallaan, ja joko hyväksytään (jos tämän ajatellaan olevan paras), tai hylätään ennen seuraavan kandidaatin haastattelua. Hylättyä kandidaattia ei voi saada takaisin, ja kun kandidaatti on joko hylätty tai hyväksytty, prosessi lakkaa. Viimeinen kandidaatti on pakko hyväksyä oletuksena jos prosessi ei ole siihen mennessä päättynyt.

a. Miten perillinen maksimoi mahdollisuutensa valita paras kandidaatti, olettaen että mitään siteitä ei ole?

Tilanne vaatii, että perillinen hylkää tietyn määrän kandidaatteja ehdottomasti (“hylkäysvaihe”), mitä seuraa “valintavaihe”, jossa hän valitsee ensimmäisen jäljelle jääneistä kandidaateista, joka on parempi kuin kukaan aiemmin hylätyistä. Mahdollisuudet valita paras kandidaatti maksimoituvat, kun hylkäysvaihe on tietyn pituinen. Todennäköisyys pienenee jos hylkäysvaihe on liian pitkä (paras kandidaatti tulee todennäköisemmin hylätyksi) tai liian lyhyt (hänellä ei ole tarpeeksi kokemusta järjestellä kandidaatteja asianmukaisesti, mistä seuraa, että huonompi kandidaatti tulee hyväksytyksi).

Tämä tunnetaan “optimipysäytyksen” ongelmana, ja e näyttäytyy ratkaisussa johtuen sen optimiominaisuudesta. Suurilla kandidaattien n lukumäärillä, optimaalinen lukumäärä kandidaatteja, joka tulee alkuvaiheessa hylätä, tulisi olla n jaettuna e:llä.

Tässä on todennäköisyyslaskelmat, kun n = 10 jos hylkäysvaihe (r) = 3. Ensinnäkin, huomaa että paras kandidaatti saattaa tulla missä kohtaa tahansa 10:sta haastattelusta, ja todennäköisyys olla missä tahansa kohdassa on 1/10 (1 / n). Jokaiselle haastateltavalle, joka on järjestysluvulla (i), me kerromme tämän 1/10 todennäköisyydellä, että paras kandidaatti tulee valituksi tämän järjestysluvun kohdalta. Sitten summaamme todennäköisyydet yhteen kaikille sijainnille ja näin saamme yleisen kaavan.

Jos paras kandidaatti on sijainneilla 1-3, hänet hylätään automaattisesti. Todennäköisyys (p) valita paras kandidaatti = 1/10 × 0 = 0.
Jos paras kandidaatti on sijainnilla 4, hänet valitaan aina. Todennäköisyys p tälle lopputulemalle = 1/10 × 1 = 1/10 = 1/n.
Sijainnilla 5, kandidaatti valitaan mikäli aiempi paras kandidaatti on ollut sijainneilla 1-3, mutta ei sijannilla 4. Joten p = 1/10 × 3/4 = 1/n × r/(i–1) = r/n × 1/(i–1).
Sijainnilla 6, kadidaatti valitaan, jos aiempi paras kandidaatti oli sijainneilla 1-3, mutta ei sijainneilla 4 tai 5. Joten p = 1/10 × 3/5 = 1/n × r/(i–1) = r/n × 1/(i–1).
…
Sijainnilla 10, p = 1/10 × 3/9 = 1/n × r/(i–1) = r/n × 1/(i–1).

Kuten voimme nähdä, saamme saman ilmaisun jokaiselle sijainnille valintavaiheessa: r/n × 1/(i–1). Kaava sijainnille 4 voidaan kirjoittaa muotoon 1/10 × 3/3 = r/n × 1/(i–1).

Ottamalla r/n pois summasta, tämä summa — todennäköisyys löytää paras kandidaatti — voidaan kirjoittaa:

Vastaavasti todennäköisyys löytää paras kandidaatti r = 4 alkukandidaattien tullessa hylätyksi on 39.8%. Nämä ovat kaksi suurinta arvoa, ja todennäköisyys pienenee suuremmilla tai pienemmillä hylkäysvaiheilla. Muistuttaako tämä ositusongelmaa? Se ei ole yhteensattumaa, kuten seuraavaksi näemme.

b. Miten perillisen todennäköisyys muuttuu jos on 10% todennäköisyys, että ensimmäisellä sijainnilla on tasapeli?

Koska perillisellä on nyt kaksi yhtä vahvaa kandidaattia 10% ajasta, todennäköisyys löytää paras kandidaatti kasvaa.

c. Tämä ongelma on klassinen, jonka ratkaisu liittyy e:hen. Voitko selittää miten e liittyy tähän?

Osoittautuu, että e astuu kuvioon kaksi kertaa tässä ongelmassa! Kun lukumäärä n kasvaa, Neperin luku tulee esiin sekä todennäköisyydessä löytää paras kandidaatti että kuinka monta kandidaattia hylätä alussa.

Yllä johdettu todennäköisyyskaava voidaan esittää, kun n kasvaa äärettömyyteen, integraalilla korvaamalla suhteen r/n (hylkäysten suhde) raja-arvo x:llä, korvata termi (i–1)/n (inkrementaalinen todennäköisyys jokaiselle n) p:llä ja 1/n (muutosnopeus yhdestä kokonaisluvusta toiseen) dp:llä. Tämä antaa todennäköisyyden raja-arvoksi:

x ∫_x¹1/p dp = −x lnx.

Taaskin oikeanpuoleinen ilmaisu on samanlainen kuin aiemmin ositusongelmassa tarkastelemamme. Asettamalla derivaatan nollaksi saamme, että optimisuhde hylättäville kandidaateille ja todennäköisyys paran valinnan tekemiselle on 1/e, eli arviolta 36.8%.

d. Miten perillinen voi saavuttaa korkeimman odotetun vahvuuden valitsemalleen kandidaatille tässä käytännöllisemmässä valintaskenaariossa?

Yllä esitetyssä klassisessa skenaariossa perillinen ottaa käyttöön kaikki-tai-ei-mitään -strategian hylkäämällä ensimmäiset kandidaatit ja sitten valitsemalla ensimmäisen, joka parantaa hylättyjen laatua. Vaikka tämä maksimoikin todennäköisyyden löytää parhaimman kandidaatin, se voi myös johtaa siihen, että jäädään jumiin matalan tason kandidaatin kanssa jos paras kandidaatti oli hylättyjen joukossa. Tämän välttämiseksi hänen paras strategia on olla erittäin vaativa heti alusta lähtien ja etsiä parasta kandidaattia, ja sitten laskea rimaa ja tyytyä hyvään kandidaattiin niiden määrän ehtyessä.

Tämä strategia voidaan esittää tarkasti aloittamalla lopusta, jossa on vain yksi kandidaatti jäljellä. Tämä henkilö saattaa olla kuinka hyvä vain yhtä suurella todennäköisyydellä. Joten odotusarvo on, että viimeinen kandidaatti on keskiarvoisen hyvä (tässä tapauksessa 5.5). Joten sinun tulisi hyväksyä toisiksi viimeinen kandidaatti, jos tämä on viiden parhaan joukossa, vaikka hän ei olisikaan paras. Kun kaksi kandidaattia on jäljellä, odotusarvo paremmalle näistä on arviolta 3.67, joten kolmannesta kandidaatista viimeiseen sinun kannattaisi tyytyä kandidaattiin, joka on kolmen parhaan joukossa. Laskemalla tarkalleen miten korkea rima sinulla tulee kussakin vaiheessa sinulla on parempi todennäköisyys saada erittäin hyvä kandidaatti, verrattuna klassisen algoritmin käyttöön.

Pulma 3: Yhdessäolo

Suureen auditorioon järjestetään show, joka hyväksyy vain pariskuntia. Kun pariskunta tulee auditorioon, he valitsevat satunnaisesti vierekkäiset paikat. Jokainen uusi pariskunta tekee samoin, ja monta kertaa tämä johtaa tyhjiin penkkeihin pariskuntien välillä. Istumapaikkoja jaetaan kunnes jäljellä on enää yksittäisiä tyhjiä paikkoja. Sitten auditorio julistetaan täydeksi, ja show alkaa.

a. Kuinka paljon penkeistä odotetaan jäävän tyhjiksi kun auditorio julistetaan täydeksi?

Vastaus, kun penkkien lukumäärä kasvaa, lähestyy lukua e^-2, eli arviolta 13.5%.

b. Miten e liittyy tähän yhdessäolon teatteriin?

Katsotaan mitä tapahtuu, kun on pieni määrä penkkejä, jotka on merkitty kirjaimin. Kutsutaan tyhjien penkkien odotusarvoa luvuiksi E₁, E₂, E₃, E₄ ja niin edelleen, jossa alaindeksi kertoo sen miten monta tyhjää penkkiä kullakin rivillä on.

Yksittäinen penkki on tyhjä: pariskunta ei voi mennä siihen, joten E₁ = 1.
Jos on kaksi penkkiä, siihen voi pariskunta mennä, joten E₂ = 0.
Kolmeen penkkiin pariskunta voi istua AB tai BC, ja yksi penkki jää tyhjäksi kummassakin, joten E₃ = 1.
Neljässä penkissä pariskunta voi istua BC, jolloin jää kaksi tyhjää penkkiä, tai he voivat istua AB tai CD, ja tyhjäksi ei jää yhtään. Tästä saadaan yhteensä kaksi tyhjää penkkiä ja odotusarvoisesti E₄ = 2/3.

Leikkimällä näiden muutaman numeron välisillä suhteilla, Lazar Ilic ja Michel Nizette onnistuivat johtamaan rekursiokaavan jolla he kykenivät ennustamaan tyhjien penkkien määrän nykyisestä penkkien määrästä (n) käyttämällä aiempia tuloksia n – 1 ja n – 2. Kaava on (kun n ≥ 2):

(n − 1)E_n = 2nE_n₋₂+ (n − 2)E_n_-1.

Sarja käyttäytyy: 1, 0, 1, 2/3, 1, 16/15, 11/9, 142/105 …

Nämä luvut jaettuna penkkien määrällä antavat suhteellisen tyhjien penkkien suhteellisen osuuden, jonka Nizette laski olevan 16.24% 10 penkille, 13.804% 100:lle, 13.561% 1000:lle ja 13.538% 6000:lle. Voit nähdä, että lukema lähestyy arvoa e^-2 eli 13.5335…%. Mutta miten voimme tietää, että se suppenee tuohon arvoon suurille luvuille, joiden suhteen laskeminen kestää liian kauan?

Rekursiokaava on hyvä, mutta se on kuin yrittäisi kiivetä ääretöntä portaikkoa yksi askel kerrallaan. Me tarvitsemme suljetun muodon ratkaisun, joka riippuu ainoastaan n:sta. Suljetun muodon kaava on kuin hissi. Painat nappia mille tahansa n:lle, ja suih! — hissi vie sinut sinne, vaikka rakennus onkin ääretön.

Suljetun muodon kaavan selvittäminen rekursioyhtälöstä tarkoittaa rekursion ratkaisua. Tälle ei ole olemassa maagista ratkaisua, ja vaikka joitain tekniikoita onkin olemassa, joita kokeilla, se on eräänlainen taiteenlajinsa. Matemaattisissa ohjelmistoissa kuten Mathematica on omat pakettinsa tätä varten. Meidän ongelmassamme Lazar Ilic tuotti suljetun muodon ratkaisun E_n:lle, joka kertoo raja-arvon e^-2 olevan oikein.

Joten e tulee kuvioon mukaan, mutta miten? Meillä ei edelleenkään ole käsitystä siitä, miten se sinne päätyi. Mitä voimia se käytti? Alla yritän intuitiivisesti avata tätä.

Johdetaan ensin kaksi differenssiyhtälöä omasta sarjastamme E. Ensimmäisen asteen differenssisarja D koostuu kahdesta peräkkäisestä E:n arvosta, ja toisen asteen differenssisarja DD koostuu eroista kahden D:n arvon välillä. Näin D₁ = E₁ − E₀, D₂ = E₂ − E₁, D₃ = E₃ − E₂ ja niin edelleen, ja DD₁ = D₁ − D₀, DD₂ = D₂ − D₁, DD₃ = D₃ − D₂ ja niin edelleen. (Sekä E₀ ja D₀ ovat 0). Selitän tämän kaiken pointin kohta. Alkuarvot kaikelle kolmelle sarjalle on esitetty alla.

n	Tyhjien penkkien odotusarvo E	Arvo	1. diffyht. D	Arvo	2. diffyht. DD	Arvo
0	E₀	0	D₀	0	DD₀	0
1	E₁	1	D₁ = E₁ – E₀	1	DD₁ = D₁ – D₀	1
2	E₂	0	D₂ = E₂ – E₁	-1	DD₂ = D₂ – D₁	-2
3	E₃	1	D₃ = E₃ – E₂	1	DD₃ = D₃ – D₂	2
4	E₄	23	D₄ = E₄ – E₃	–13	DD₄ = D₄ – D₃	–43
5	E₅	1	D₅ = E₅ – E₄	13	DD₅ = D₅ – D₄	23
6	E₆	1615	D₆ = E₆ – E₅	115	DD₆ = D₆ – D₅	–415
7	E₇	119	D₇ = E₇ – E₆	745	DD₇ = D₇ – D₆	445

Rekursioyhtälöä muokkaamalla voimme johtaa suljetun muodon kaavan DD_n:lle seuraavasti (n ≥ 1):

DD_n = (-2)^n-1 / (n-1)!

Voimme varmistaa kaavan toimivan vertaamalla sitä yllä olevaan taulukkoon:

DD₁ = (-2)⁰ / 0! = 1
DD₂ = (-2)¹ / 1! = -2
DD₃ = (-2)² / 2! = 2
DD₄ = (-2)³ / 3! = -8 / 6 = -4 / 3
DD₅ = (-2)⁴ / 4! = 16 / 24 = 2 / 3
DD₆ = (-2)⁵ / 5! = -32 / 120 = -4 / 15
DD₇ = (-2)⁶ / 6! = 64 / 720 = 4 / 45

Tässä on homman pointti: Huomaa mitä tapahtuu, kun kaikki DD:t summataan.

DD₁ + DD₂ + DD₃ + … + DD_n₋₁ + DD_n =

D₁ − D₀ + D₂ − D₁ + D₃ − D₂ + … + D_n₋₁ − D_n₋₂ + D_n − D_n₋₁ = D_n − 0 = D_n.

Kaikki muut termit kumoutuvat, ja jäljelle jää vain D_n. Tätä rekursioyhtälön ratkaisutekniikkaa kutsutaan teleskooppiratkaisuksi.

Laitetaan suljetun muodon kaava takaisin jokaiseen DD:n.

D_n = 1 – 2 / 1! + 2² / 2! − 2³ / 3! + 2⁴ / 4! − 2⁵ /5! + ⋯ .

Näyttääkö tutulta? Vertaa tätä alkuperäiseen yllä esitettyyn e^-x:n äärettömään sarjaan. Itse asiassa suurella n, tämä on tarkalleen e^-2.

Joten transendentaalisen vakiomme neliö on maagisesti ilmestynyt ensimmäisen sarjan nimittäjään, joka johdettiin tyhjien penkkien määrälle. Se on siellä, koska prosessissa summataan -2:n potensseja, jotka jaetaan samalla kertomalla, ja nämä ovat tarkalleen e:n sarjakehitelmän termit.

Me joudumme silti työstämään D-sarjaa saadaksemme samanlaisen ilmaisun E_n:lle. Tämä arvo, jaettuna n:llä,antaa meille tyhjien penkkien suhdeluvun. Loppusuoran saavuttamiseksi pitää vielä kikkailla algebrallisesti. Riittää todeta, että e⁻² pysyy lopullisessa kaavassa, joka näyttää tältä:

E_n / n = e^-2 + 2e^-2n^-1 + …

Suurilla n, ainoastaan ensimmäinen termi jää jäljelle, josta saammejo selvittämämme tuloksen e^-2. Huomaa suuret mutta äärelliset luvut, jotka Michel Nizette listasi, pelkkä kahden ensimmäisen termin summa sopii melkein täydellisesti tyhjien penkkien suhdelukuun.

Artikkelin julkaissut Quanta Magazine

Tiede

Kuinka saada selkoa kaaoksesta

20 huhtikuun, 2023 paatoimittaja Kommentoi

Vuonna 1885 Ruotsin kuningas Oscar II ilmoitti julkisesta haasteesta, joka koostui neljästä matemaattisesta ongelmasta. Ranskalainen matemaatikko Henri Poincaré keskittyi yhteen niistä, joka liittyi taivaankappaleiden liikkeisiin, niinkutsuttuun n-kappaleen ongelmaan. Jatkaako aurinkokuntamme kellonkaltaista liikettään ikuisesti, vai lentävätkö planeetat pois kauas tyhjyyteen, vai törmäävätkö ne Aurinkoon ja tuhoutuvat?

Poincarén ratkaisu — jossa ainakin jotkut systeemit, kuten Aurinko, Maa ja Kuu, olivat vakaita — voitti nimekkään palkinnon, ja ratkaisuartikkeli painettiin julkaistavaksi vuonna 1889. Valitettavasti hänen ratkaisunsa oli väärä.

Poincaré myönsi virheensä ja maksoi siitä, että hänen ratkaisun painokappaleet tuhottaisiin (mikä maksoi enemmän kuin voitettu rahapalkkio). Kuukautta myöhemmin hän jätti korjatun version. Nyt hän näki, että jokainen systeemi, jossa on ainoastaan kolme kappaletta, käyttäytyi liian ennustamattomasti — liian kaoottisesti — jotta sitä voitaisiin mallintaa. Ja tästä sai alkunsa dynaamisten systeemien ala.

Meidän tarkoituksiimme dynaaminen järjestelmä on yksinkertaisesti funktio, jonka mahdolliset ulostulot voivat myös toimia syötteinä. Tämä mahdollistaa meidän takaisinkytkeä ulostulot syötteiksi useaan kertaan, ja näin systeemin käyttäytyminen kehittyy. Kuten Poincarén ratkaisu näyttää, tämä yksinkertainen oletus voi tuottaa esimerkkejä, jotka ovat niin monimutkaisia ja satunnaisia, että niitä kutsutaan kaoottisiksi.

Elegantti tapa ymmärtää Poincarén johtopäätös, ja samalla tuoda hieman järjestystä kaaokseen, saatiin 70 vuotta myöhemmin. Pian sen jälkeen, kun nuori ja välkky topologi (ja tuleva Fieldsin mitalin saaja) Stephen Smale kirjoitti ensimmäisen artikkelinsa dynaamisista järjestelmistä, hän sai kirjeen, joka johti hänet keksimään suhteellisen yksinkertaisen ja ubiikin funktion, joka selitti Poincarén havaitseman kaaoksen kolmen kappaleen ongelmassa. Smale kutsui tätä hevosenkengäksi.

Tämän ymmärtämiseksi aloittakaamme suhteellisen yksinkertaisella dynaamisella systeemillä, joka ei ole kaoottinen. Oletetaan, että haluat laskea 2:n neliöjuuren yksinkertaisella nelilaskimella. Newtonin menetelmä sanoo, että voit aloittaa millä tahansa arvauksella tuloksesta — sanokaamme vaikka 3 — ja laittaa sen funktioon f (x) = x/2 + 1/x. Tulos, f (3) = 1.8333333, on lähempänä oikeaa arvoa kuin syöte. Päästäksemme vieläkin lähemmäksi, laitamme tuloksen takaisin funktioon: f (1.8333333) = 1.4621212. Näin kun tekee vielä kolme kertaa saadaan 1.4142136, todennäköisesti tämä on laskimesi tarkkuuden raja.

Kuudennen approksimaation merkitseminen f(f(f(f(f(3)))) on vaivalloista, joten sen sijaan me kirjoitamme f⁵(3), ja me kutsumme ääretöntä funktion tulosten sarjaa x:n “ympäristöksi”. Se auttaa, kun ajattelee jokaista iteraatiota kellon pyörähdyksenä, ja pitää ympäristöä lukujonolla hyppimisenä kunnes me pääsemme lukuun √2.

Sekä 3:n että 1/2:n ympäristöt molemmat lähestyvät kiintopistettä √2. kuva: Samuel Velasco/Quanta Magazine

Tässä esimerkissä me nimitämme lukua √2 puoleensavetäväksi kiintopisteeeksi: se on kiintopiste, koska se tuottaa kiinteän ympäristön √2, √2, √2…, ja puoleensavetäväksi, koska mustan aukon tavoin se imee itseensä kaikkien lähiympäristöjen pisteet.

Mutta kaikki dynaamiset systeemit eivät käyttäydy tällä tavoin ennustettavasti ja yksinkertaisesti. Dynaamisella järjestelmällä voi olla ympäristöjä, jotka kiertävät syklisesti rajallisen pistejoukon läpi, sinkoavat äärettömyyteen tai eivät käyttäydy mitenkään järjestelmällisesti.

Näiden konseptien ymmärtämiseksi, joka siis on keskeistä kaoottisille järjestelmille, tarkastelkaamme erityisen valaisevaa esimerkkiä nimeltä telttakuvaus, T, joka on määritelty x:n arvoille välillä 0…1. Vähän samalla tavoin, kuin toffeeta valmistettaessa se venyy tuplapitkäksi, sitten se taitetaan puolivälistä kahtia ja asetetaan takaisin alkuperäiseen pituuteen. Tämä tarkoittaa, että 0 ja 1 molemmat kuvautuvat nollaan ja 12 kuvautuu ykköseen. Koska telttakuvauksen tuottamat arvot ovat myös nollan ja ykkösen välillä, se voi olla dynaaminen järjestelmä. Funktion iterointi Newtonin menetelmällä tarkoittaa tämän venyttämisen ja taittamisen prosessin toistoa.

Telttakuvaus, jonka yhtälö on T(x)= −2∣x−1/2∣ + 1, venyttää ja taittaa välin [0, 1]. Funktion iterointi tarkoittaa toistuvia venytyksiä ja taitoksia.

Niinkuin esimerkissämme √2, telttakuvauksella on kiintopisteet 0 ja 23. Mutta sillä on myös ympäristö, joka vaihtelee kahden pisteen välillä, 25 ja 45 — me kutsumme tätä kakkosperiodin ympäristöksi — ja kolmosperiodin ympäristö pyörii arvojen 29, 49 ja 89 läpi. Yllättävää kyllä, koska telttakuvauksella on piste, joka tuottaa kolmannen periodin ympäristön, me voimme osoittaa, että sillä on piste jokaisella periodilla — huolimatta siitä minkä positiivisen kokonaisluvun valitsee, aina tulee olemaan toistuva ympäristö ja yhtä monta pysähdystä polulla.

Tämän reaalilukualueen funktioiden ominaisuuden löysi ensimmäisenä ukrainalainen matemaatikko Alexander Sharkovsky. Kuitenkin hänen vuoden 1964 tutkielmansa tästä aiheesta on pysynyt Itä-Euroopan ulkopuolisille tuntemattomana, ja ainoa tulos joka on tiedossa on Marylandin yliopiston matemaatikoilta Tien-Yien Li ja James Yorke, jotka toisistaan riippumatta löysivät sen vuonna 1975. He osoittivat, että sellaisella dynaamisella järjestelmällä on myös ympäristöjä, jotka eivät käyttäydy mitenkään järjestelmällisesti, niinkuin pisteen √2 – 1 kymmenennen kuvauksen ympäristö. He kirjoittivat, että “kolmas periodi tarkoittaa kaaosta”, ja näin ottivat käyttöön matemaattisen termin “kaaos” siinä samassa.

Ympäristö √2 – 1 kymmenennelle kuvaukselle ei näytä mitään selkeää kuviota.

Vaikka pisteet √2 – 1 ja √2 – 0.999 ovat lähellä toisiaan, niiden ympäristöt erkanevat nopeasti: esimerkiksi T⁹(√2 – 1) = 0.07734 kun taas T⁹(√2 – 0.999) = 0.58934. Tämä ilmiö tunnetaan nimellä “alkuarvoista riippuva herkkyys” tai virallisemmin nimellä perhosvaikutus. Pienillä alkuarvojen muutoksilla voidaan saada suuria loppumuutoksia aikaan. Matemaatikko ja meteorologi Edward Lorenz esitti asian, “Aiheuttaako perhosen siivenisku Brasiliassa tornadon Teksasissa?” Vaikka kaaokselle ei ole mitään vakiintunutta määritelmää, tämä herkkyystarkastelu on yksi sen tunnusmerkki.

Ymmärtääksemme kaoottisia järjestelmiä — ja Smalen hevosenkenkää — käyttäkäämme aluksi karkealta näyttävää tekniikkaa. Jaetaan mahdollisten arvojen väli puolikkaisiin nimeltä L ja R. Sitten, kun ympäristö etenee, yksinkertaisesti havaitaan kummalle puolikkaalle seuraava iteraatio osuu. Tämä sarja on ympäristön “kulkureitti”. Esimerkiksi, kolmannen periodin luvun 29 ympäristön kulkureitti on LLRLLRLLR… koska 29 ja 49 ovat L:llä ja 89 on R:llä. Ympäristön √2 – 1 kulkureitti alkaa LRLRRRRRLL.

Telttakuvauksessa piste 29 tuottaa kolmosperiodin ympäristön kulkureitillä LLRLLRLLR…, ja piste √2 – 1 tuottaa kulkureitin, joka alkaa LRLRRRRRLL…

Ympäristöjen esittäminen kulkureiteillään näyttää siltä kuin informaatiota häviäisi paljonkin, mutta niin ei tapahdu. Se johtuu siitä, että jokainen L:n ja R:n sarja vastaa yhtä ja vain yhtä pistettä. 29:n ympäristö on esimerkiksi ainoa, jonka kulkureitti on LLRLLRLLR…. Tämä ominaisuus tarjoaa kätevän työkalun analysoida telttakuvauksen dynamiikkaa. Se paljastaa, että pisteet ovat periodisia juuri silloin, kun kulkureitit ovat sitä. Se myös mahdollistaa meidän määrittää pisteen sijainnin mistä tahansa kulkureitistä.

Laajennetaan nyt telttakuvauksen ideaa useampaan ulottuvuuteen, ja viimein pääsemme Smalen hevosenkenkäfunktioon h. Aloitetaan neliöllä, venytetään se nelikulmioksi, taitetaan se hevosenkengäksi ja asetetaan se alkuperäisen neliön päälle.

Smalen hevosenkenkäkuvaus venyttää ja taittaa neliön itsensä päälle.

Niinkuin kaikkien dynaamisten järjestelmien kanssa, me iteroimme tätä prosessia — venytä, taita, venytä, taita, venytä, taita — ja se tuottaa hevosenkenkiä hevosenkenkien sisään.

Smalen kuvauksen iterointi tuottaa sisäkkäisiä hevosenkenkiä.

Hevosenkenkäkuvaus on kääntyvä — sen lisäksi, että tietää minne piste x on menossa, jota h(x) kuvaa, me tiedämme mistä se oli tulossa, jota kuvaa h^-1(x). Soveltamalla h^-1:a alkuperäiseen neliöön syntyy uusi hevosenkenkä, joka on suorassa kulmassa ensimmäiseen nähden. Jos jatkat soveltamista, saat lisää hevosenkenkiä uuden sisään.

Kun nämä kuvaukset laitetaan päällekkäin:

Hevosenkenkäkuvaus on kääntyvä, mikä tuottaa kaksi toisiinsa nähden suorassa kulmassa olevaa hevosenkenkää.

On olemassa pistejoukko, jota kutsumme nimellä H, joka koostuu kaikkien vaaka- ja pystysuuntaisten hevosenkenkien leikkauksista. Tässä kohtaa tapahtuu mielenkiintoisia asioita.

Erittäin epäyhtenäisen joukon H pisteet, jotka pysyvät neliöiden sisällä jatkuvasti, ovat sisäkkäisten hevosenkenkien h ja h^-1 leikkauspisteissä.

Aivan kuten telttakuvauskin, hevosenkenkäkuvausta voidaan analysoida kulkureittien avulla. Määritellään L pystysuoran hevosenkengän vasemmaksi puoleksi ja R oikeaksi puoleksi.

Me merkitsemme hevosenkengän vasenta ja oikeaa puolta L:llä ja R:llä, ja käytämme näitä nimiä H:n ympäristöjen kulkureittien esittämiseen.

Jos me otamme minkä tahansa pisteen H:sta, me voimme laskea kulkureitin sen eteenpäin vievästä ympäristöstä. Ja koska hevosenkenkä on kääntyvä, me voimme määrittää kulkureitin taaksepäin vievästä ympäristöstä myös.

Esimerkiksi, sanokaamme, että voimme aloittaa pisteestä L-alueella ja kun me menemme eteenpäin ympäristössä, saamme LRRLRR…, mikä jatkuu äärettömyyteen. Kun me menemme taaksepäin ympäristössä, me saamme LRRLRR…. Joten me voimme kirjoittaa kulkureitin …LRRLRRLRRLRR…, jossa alleviiva merkitsee lähtöpistettä. Tämä on kolmosperiodin ympäristö.

Tehdään tämä nyt kaikille pisteille H:ssa.

Hevosenkengällä on jokaisen periodin periodiset pisteet, ja periodisuus näkyy kulkureiteissä.

Kulkureittien avulla saamme täyden kuvauksen hevosenkenkäfunktiosta — me ymmärrämme sen täysin — vaikka (niinkuin telttakuvauksen kanssa) sillä on kaoottinen dynamiikka: periodisia pisteitä, alkuarvoista riippuvia herkkyyksiä jne.

Nyt voimme nähdä miten Smalen hevosenkenkä voi kuvata selvemmin kaaosta Poincarén kolmen kappaleen ongelmaan. Hänen kaoottisessa hevosenkengässä tulee olla kiintopiste (kutsutaan sitä nimellä p) jonka kulkureitti on …LLLLLLL…, koska kaikkien mahdollisten kulkureittien pisteet ovat olemassa. Tämän pisteen eteenpäin vievä ympäristö lähestyy p:tä (me sanomme “tulevaisuuteen”), kuten myös sen taaksepäin vievä ympäristö (“menneisyyteen”).

Smalen hevosenkenkä, piste q, kulkureitti …LLLRLLL…, lähestyy kiintopistettä p, jonka kulkureitti on …LLLLLLL…, sekä tulevaisuudessa että menneisyydessä.

Kuitenkin Poincaré oli havainnut, että joidenkin funktioiden kiintopisteillä on sekä puoleensavetävä että hylkivä suunta. Tämä tarkoittaa, että on olemassa pistekäyrä, joka liikkuu kohti kiintopistettä, kuin laskimo joka palauttaa verta sydämeen, ja pistekäyrä, joka on liikkumassa poispäin, kuin valtimo, joka vie verta pois sydämestä. Jos nämä käyrät leikkaavat, niiden leikkauspisteillä, joita kutsutaan homokliinisiksi pisteiksi, on mielenkiintoinen ominaisuus, että ne lähestyvät kiintopistettä sekä tulevaisuudessa että menneisyydessä.

Piste q on homokliininen piste, koska se lähestyy kiintopistettä p sekä eteenpäin että taaksepäin mentäessä. Kun tämä tapahtuu, käyrät tuottavat homokliinisen vyyhdin ja ne käyttäytyvät kaoottisesti — niinkuin hevosenkengässä.

Smale huomautti, että q on homokliininen piste, koska sen ympäristö lähestyy p:tä sekä tulevaisuudessa että menneisyydessä. Smale myös osoitti päinvastaisen: jos on homokliininen piste (kuten Poincarélla oli), silloin on myös hevosenkenkä. Ja koska me tiedämme, että hevosenkengät ovat kaoottisia, Poincarén systeemin on oltava samalla tavalla kaoottinen. Toisin sanoen, Poincarén monimutkainen järjestelmä — ja mikä tahansa järjestelmä, jolla on homokliininen piste — käyttäytyy kuten Smalen yksinkertaisempi systeemi. Jos ymmärtää hevosenkengän, ymmärtää itse kaaoksen.

Smale osoitti myös, että tämä kaaos on robusti. Jos me kuvaisimme neliön hieman erilaiselle hevosenkengälle, syntyvällä kuvauksella olisi identtinen kaoottinen käyttäytyminen. Huolimatta systeemin paikallisesta epävakaudesta, globaali käyttäytyminen on äärimmäisen vakaata. Eli, tämä kaaos ei ole häipyvää, edes pienillä häiriöillä. Kaaos itsessään osoittautuu olevan vakaa.

Kaaosteoria jatkoi suosion kasvattamista. Se esitettiin “tieteellisen mallintamisen uutena paradigmana” vuoden 1986 Scientific Americanin artikkelissa, James Gleickin vuoden 1987 julkaistun menestyskirjan Chaos provokatiivisella alaotsikolla: “Making a New Science.” Kaaos pääsi mukaan pop-kulttuuriin mm. vuoden 1990 uudessa Jurassic Park –elokuvassa sekä Tom Stoppardin vuoden 1993 näytelmässä Arcadia.

Vaikka jotkut matemaatikot toppuuttelivat hypeä — dynaamiset systeemit eivät olleet mitään uutta — kaoottisten järjestelmien vaikutus matematiikkaan ja tieteeseen oli perinpohjainen. Kaaoksen olemassaolo näytti, että jopa deterministissä järjestelmissä me saatamme olla kyvyttömiä tarkkaan ennustamaan tulevaa, johtuen alkuarvoista riippuvasta herkkyydestä. Mutta Smalen hevosenkengän kaltaisten työkalujen ansiosta me voimme edelleen saada hyödyllistä tietoa näistä järjestelmistä.

Artikkelin julkaissut Quanta Magazine

Tiede

Opi graafiteoriaa tämän seurapelin avulla

22 joulukuun, 2022 paatoimittaja Kommentoi

Nyt kun pandemiarajoitukset ovat helpottaneet, ihmiset ovat alkaneet tavata toisiaan jälleen kasvotusten. Mutta koska tapaamisesta on hetki, jos ystäväsi tarvitsevat jotain millä rikkoa jää, tässä on matemaattinen peli jota voi kokeilla.

Haasta kaikki kättelemään toisia ryhmässä, mutta vain parittoman määrän ihmisiä kanssa. (Kättely voi myös olla jokin muu kahdenvälinen tervehdys, esim. läpy.) Olettakaamme että ryhmässänne on sinä ja kuusi muuta ystävää.

Sanokaamme, että Anna ja Byron kättelevät toisiaan. Nyt kummallakin on yksi kättely.

kuva: Merrill Sherman/Quanta Magazine

Caitlin haluaa liittyä mukaan, joten hän kättelee Byronia kerran, joka on pariton luku. Mutta nyt Byronilla on kaksi kättelyä, joten hänen lukemansa on parillinen.

Demarr, Ernest ja Flora kättelevät myös kerran ja he muuttavat jokaisen parillisen määrän kätelleen parittomaksi ja parittoman parilliseksi.

Lopulta kuusi ystävää keksivät miten tämä ratkeaa, ja päätyvät hyväksyttävään ratkaisuun.

Mutta sinun pitää silti kätellä jotain toista, ja ylimääräinen kättely merkkaa. Kun kättelet jotain, jollain ystävälläsi on nyt parillinen lukumäärä kättelyitä. Ja näin peliä pitää jatkaa.

Ylläoleva kuva esittää pelin graafina — pisteiden joukkona (solmut) ja niiden välisinä viivoina (kaaret). Sinun dilemmasi toimii esimerkkinä yksinkertaisesta, mutta perustavanlaatuisesta ideasta graafiteoriassa, matematiikan alalla joka tutkii näiden representaatioiden ominaisuuksia. Vaikka monet graafiteorian tärkeät perusperiaatteet on keksitty jo satoja vuosia sitten, nykypäivän tieteilijät silti käyttävät niitä ymmärtääkseen paremmin sitä miten erilaiset järjestelmät kytkeytyvät toisiinsa, poliittisissa verkostoissa ja eläinten ekosysteemeissä ja internetin verkkosivuilla. Myös tätä peliä jota nyt pelaamme tutkitaan.

Oman pelimme graafissa ihmiset ovat solmuja ja kättelyt ovat kaaria. Numerot kuvaavat sitä miten monta kättelyä henkilöllä on, joka graafissa on tietyn solmun ”asteluku”: se on kunkin pisteeseen kytkeytyneiden kaarien lukumäärä.

Solmuja ja niiden astelukuja

Matemaatikkojen tutkimat graafit voivat muuttua suuriksi ja monimutkaisiksi, joten auttaa kun on joitain yksinkertaisia piirteitä, joita etsiä. Eräs tällainen piirre on graafin kaikkien astelukujen summa. Heti suoraan ”astelukusumma” kertoo meille, että seitsemällä pelaajalla pelimme on mahdotonta voittaa! Tarkastellaan hieman syytä.

Yksi tapa laskea graafin astelukusumma on listata kaikki yksittäiset asteluvut ja summata ne yhteen. Mutta toinen tapa nojaa välkkyyn kirjanpitoon kaarista. Koska jokainen kaari yhdistää kaksi solmua, sen kontribuutio kokonaissummaan on kaksi: yksi kummallekin solmulle joissa se on kiinni. Joten graafin astelukujen summaaminen on sama kuin laskisi jokaisen kaaren kaksi kertaa. Koska astelukusumma on kaksi kertaa kaarien määrä, mille tahansa graafille pätee, että summa on aina parillinen luku.

Näin pelimme on tuomittu epäonnistumaan. Mieti graafia, jonka me haluaisimme rakentaa voittaaksemme pelin: pitää olla seitsemän ihmistä ja seitsemän paritonta astelukua. Etsitään nyt astelukusumma: lisää ensimmäiset kaksi astelukua keskenään ja saamme parillisen luvun. Ja sen jälkeen seuraavaa summatessa saamme parittoman luvun. Ja sitten parillisen jne. Jos summaa parittoman määrän parittomia lukuja, summan on pakko olla pariton. Mutta koska minkä tahansa graafin astelukusumman pitää olla parillinen, me emme mitenkään voi rakentaa graafia, jolla olisi paritonta määrää parittomia kaaria. Peliämme ei voi voittaa.

Toisaalta, on mahdollista voittaa peli, jos on parillinen määrä pelaajia. Me näimme sen heti ensimmäisessä kättelyssä sinun vuorollasi.

Me itseasiassa näimme sen jo tuota ennen: heti kun ensimmäinen pari kätteli.

Jos peliä pelaa vain kaksi, silloin on mahdollista, että kumpikin heistä kättelee parittoman määrän muita käsiä. Voit ajatella tätä paria “parittomana aligraafina”, pienempänä graafina, joka on suuremman graafin sisällä, jonka kaikki kaaret ovat asteluvultaan parittomia.

Aligraafia rakentaessa valitset joukon solmuja ja tarkastelet ainoastaan näiden solmujen välisiä kaaria. Tämä tarkoittaa, että jätät huomiotta kaaret, jotka kytkeytyvät kaikkiin aligraafin ulkopuolisiin solmuihin.

Aligraafin muodostaminen jättämällä huomiotta kaaret.

Aligraafin muodostaminen leikkaa graafin kahtia, mitä graafiteoreetikot myös tekevät analysoidessaan graafeja: se voi auttaa heitä identifioimaan solmujen ryppäitä, jotka ovat kytkeytyneet toisiinsa erikoisin tavoin. Ja kun tietää, että aligraafi on joko parillinen tai pariton, se voi antaa lisätietoa graafin rakenteesta. Esimerkiksi, parillinen graafi, joka on “yhtenäinen” — mikä tarkoittaa, että aina löydät polun minkä tahansa kahden solmun välillä — on pakko sisältää “Eulerin piiri”, polku joka kulkee jokaisen kaaren kautta vain kerran.

Omasta seurapelistämme me tiedämme, että tietylle solmujoukolle ei ole aina mahdollista muodostaa paritonta graafia. Mutta aina on mahdollista muodostaa pariton aligraafi. Eräs tylsä tapa tämän saavuttamiseksi on juuri se mitä teimme yllä: valitse kaksi solmua, jotka ovat yhdistetty toisiinsa ja jätä huomiotta kaikki muut kaaret. Siitä syntyy pariton aligraafi, erittäin pieni sellainen. Onko se aina mahdollista löytää pariton aligraafi?

On jo tiedossa, että jokainen graafi sisältää suuren parillisen aligraafin. 1960-luvulla unkarilainen matemaatikko Tibor Gallai osoitti, että jokainen graafi voidaan osittaa kahdeksi parilliseksi aligraafiksi. Se jakaisi n solmun joukon kahdeksi alijoukoksi, ja yksi alijoukoista sisältäisi ainakin puolet kaarista. Tämä takaa sen, että jokaisella graafilla on parillinen aligraafi, joka on ainakin puolet alkuperäisen koosta.

Mutta miten suuri pariton aligraafi voi olla, se on ollut tutkimusten kohteena graafiteoriassa jo 60 vuoden ajan. Epäonnistuneen seurapelimme graafissa oli pariton aligraafi, jolla oli kuusi seitsemästä solmusta.

Tämä on varsin suuri verrattuna alkuperäiseen. Mutta tässä on toinen epäonnistunut yritys pelata pienemmällä maksimaalisen parittomalla aligraafilla, sellaisella joka käyttää vain neljää alkuperäisistä solmuista.

Graafi jolla on maksimaalisen kokoinen pariton aligraafi, joka käyttää vain neljää seitsemästä solmusta.

Etsittäessä suurinta mahdollista paritonta aligraafia, varhaiset onnistumiset ilmaisivat käytettyjen solmujen lukumäärän suhteessa alkuperäisen graafin kokoon. Esimerkiksi, 1990-luvulla matemaatikko Yair Caro näytti, että millä tahansa n solmun graafilla on oltava aligraafi, joka sisältää vähintään 1/(√n) kaikista solmuista. Tämä tarkoittaa, että 25 solmun graafilla on oltava pariton aligraafi, joka sisältää ainakin 1/5 kaikista solmuista, ja 100 solmun graafilla on oltava pariton aligraafi, joka sisältää vähintään 1/10 kaikista solmuista. Samanlaisia tuloksia saatiin muitakin, mutta matemaatikot etsivät Gallain löydöstä: yksittäistä suhdelukua, joka toimii parittomille aligraafeille sillä tavalla kuin 1/2 toimii parillisille aligraafeille.

Tällainen tulos saatiin viimein vuonna 2021, kun Asaf Ferber ja Michael Krivelevich osoittivat, että jokaisella graafilla on pariton aligraafi, joka käyttää ainakin 1/10000 solmua alkuperäisen graafin solmuista. Tämä voi olla aika alhainen raja, erityisesti kun jotkut ovat spekuloineet, että todellinen raja on jossain 2/7 tietämillä, mutta yksittäisen suhdeluvun löytäminen, joka toimii, mahdollistaa matemaatikkojen osoittaa, että sellainen suhdeluku on olemassa, joka parantaa jo olemassaolevaa suhdelukua. Yksi luku, niinkuin kättely, voi merkitä paljon.

Harjoituksia

1. Etsi suurin pariton aligraafi allaolevasta graafista.

2. Näytä miten osittaa allaoleva silmukka parittomaksi ja parilliseksi aligraafiksi.

3. Täydellinen n solmun graafi on graafi, jossa jokainen n solmusta on yhdistetty kaarella kaikkiin muihin solmuihin. Voiko täydellinen graafi olla pariton graafi?

4. 1960-luvulla Tibor Gallai osoitti, että aina on mahdollista osittaa graafi kahdeksi parittomaksi aligraafiksi. Perustuen siihen mitä tässä artikkelissa olet lukenut, osaatko osoittaa, että aina ei ole mahdollista osittaa graafia kahdeksi parittomaksi aligraafiksi? Mikä on syynä?

Artikkelin julkaissut Quanta Magazine (katso myös vastaukset harjoituksiin täältä)

Tiede

Andre-Oortin konjektuuri todistettu

12 toukokuun, 2022 paatoimittaja Kommentoi

Huikeassa juuri julkaistussa todistuksessa, kolme matemaatikkoa on ratkaissut 30-vuotisen ongelman, joka tunnetaan nimellä André-Oortin konjektuuri, ja edistäneet satojen vuosien taivalta ymmärtää ratkaisuja polynomiyhtälöihin. Työ lainaa ideoita lähes kaikilta matematiikan eri osa-alueilta.

“Menetelmät, joita siinä käytetään, sanoisin, kattavat koko matematiikan”, sanoi Andrei Yafaev University College Londonista.

Uusi tutkielma alkaa erään kaikkein perustavanlaatuisimman matematiikan kysymyksen parissa: milloin polynomiyhtälöillä kuten x³ + y³ = z³ on kokonaislukuratkaisuja (positiivisia tai negatiivisia)? Vuonna 1994 Andrew Wiles ratkaisi erään version tästä kysymyksestä, joka tunnetaan Fermat’n Viimeisenä Teoreemana, eräänä 1900-luvun suurista matemaattisista voitoista.

Fermat’n Viimeisen Teoreeman ja sensellaisten ongelmien ratkaisemiseksi matemaatikot ovat kehittäneet yhä abstraktimpia teorioita, jotka tuovat mukanaan uusia kysymyksiä ja konjektuureja. Yves André ja Frans Oort esittivät kaksi tällaista pulmaa vuorollaan vuosina 1989 ja 1995, mikä johti siihen minkä me nyt tunnemme André-Oort konjektuurina. Sen sijaan että pohdittaisiin kokonaislukuratkaisuja polynomiyhtälöihin, André-Oortin konjektuuri liittyy ratkaisuihin, jotka ovat paljon monimutkaisempia geometrisia olioita nimeltään Shimuran olomuodot (engl. variety, suomennos on toimituksen ad hoc kehittämä).

Monet matemaatikot ovat työskennelleet ongelman parissa viimeiset vuosikymmenet. Vuonna 2014 Yafaev ja Bruno Klingler todistivat sen, mutta hommassa oli juju. Heidän tuloksensa riippui siitä, että Riemannin hypoteesi pätee — mutta se on eräs kuuluisa vaikea kysymys, jota ei ole edelleenkään ratkaistu.

Uusi Oxfordin yliopiston Jonathan Pilan, Wisconsinin yliopiston Ananth Shankarin ja Toronton yliopiston Jacob Tsimermanin tutkielma ratkaisee tämän. Lisäksi se näyttää Tsimermanin osaamisen, 33, jota pidetään laajalti eräänä aikansa huippumatemaatikoista.

“Jacob Tsimermanilla on kyky ymmärtää kaikkea”, Yafaev sanoo.

Erilaiset olomuodot

André-Oortin konjektuuri liittyy algebran olomuotoihin, jotka perustasollaan ovat pelkkä joukko (tai graafi) kaikista ratkaisuista yhteen polynomiyhtälöön, tai näiden kokoelma.

Yksikköympyrä on olomuoto: sen kaaren pisteiden koordinaatit ovat ratkaisuja polynomiin x² + y² = 1. Suora y = 0 on myös olomuoto. Ja näiden kahden leikkaus — pisteet (1, 0) ja (−1, 0) — on kolmas olomuoto, joka on kahden ensimmäisen sisällä.

André-Oortin konjektuurin olomuodot ovat tärkeää tyyppiä, nimeltään Shimuran olomuodot (engl. Shimura variety). Vaikka Shimuran olomuotoja on muutamaa erilaista tyyppiä, yksinkertaisin liittyy kriittiseen matemaattiseen olioon nimeltään elliptinen käyrä (yhtälöt kuten y² = x³ + 1 tai y² = x³ + 3x + 2).

Pisteet näillä Shimuran olomuodoilla koodaavat reseptin, jolla voidaan konstruoida elliptinen käyrä. Mutta on myös muita, monimutkaisempia Shimuran olomuotoja, joiden rakenne on vähemmän suoraviivainen. Niihin liittyvän informaation kuvaaminen on ollut vaikeaa.

“Yleisen tyypin Shimuran olomuotojen rakenteesta tiedetään vain vähän”, sanoo Ruochuan Liu Pekingin yliopistosta.

André-Oortin konjektuuri on juuri tuohon liittyvä kysymys: Mikä on Shimuran olomuotojen perusrakenne, joiden alle itsessään liittyy paljon modernia matematiikkaa?

Erikoispisteet

Pidetään mielessä, että olomuodot voivat elää toisten olomuotojen sisällä, samalla tavalla kuin ei-tangentiaalinen viivan ja ympyrän leikkaus luo kahden pisteen aliolomuodon. André-Oortin konjektuuri esittää kysymyksen Shimuran olomuotojen sisällä elävistä olomuodoista. Se tekee tämän keskittymällä Shimuran olomuotojen tiettyihin elementteihin.

Shimuran olomuodolla jokainen piste esittää toista olomuotoa, kuten elliptinen käyrä. Jotkut näistä käyristä ovat enemmän symmetrisiä kuin toiset, ja symmetrisempiä esitetään Shimuran olomuodolla, jota matemaatikot kutsuvat “erikoispisteiksi”.

André-Oortin konjektuuri liittyy siihen miten nämä erikoispisteet jakautuvat. Kuvittele lähteväsi liikkeelle Shimuran olomuodolla. Ajattele sitä kolmiulotteiseksi muodoksi. Seuraavaksi, piirrä käyrä sen pinnalle. Tämä käyrä on olomuoto, vaikkakaan ei välttämättä Shimuran olomuoto. Mutta André-Oortin konjektuurin mukaan, jos tuo käyrä jatkuvasti törmää erikoispisteisiin, sen on itsessään oltava Shimuran olomuoto.

“Se on eräänlainen erittäin selkeä geometrinen tulkinta”, Tsimerman sanoo.

Toisin sanoin, André-Oortin konjektuuri tekee ennusteita siitä onko pinnalla oleva käyrä Shimuran olomuoto. Silloin on olemassa yläraja erikoispisteille, joihin se voi törmätä. Matemaatikot ovat yrittäneet vuosien ajan vahvistaa Andrén ja Oortin esittämää ylärajaa. 2000-luvun ensimmäisen vuosikymmenen lopulla Jonathan Pila teki suuria harppauksia esittämällä uuden menetelmän erikoispisteiden laskemiseksi.

Pilan edistys

André-Oortin konjektuurin todistamiseksi Pila tarvitsi karkean arvion erikoispisteistä olomuodolla. Hän teki tämän antamalla pisteille ominaisuuden nimeltään “korkeus”. Korkeus mittaa miten monimutkainen tietty piste, tai arvo, on. Tarkastellaan lukuja 10 ja 10.000017. Yhtäältä ne ovat samanlaisia, mutta toisaalta ne ovat varsin erilaisia.

“Ne ovat molemmat rationaalilukuja, ja ne ovat varsin lähellä toisiaan. Mutta yksi niistä on paljon toista monimutkaisempi”, Shankar sanoo.

Yksi tapa kuvata tätä kompleksisuutta on muuttaa nämä luvut yksinkertaisiksi murtoluvuiksi. Luvun korkeus on osoittajan tai nimittäjän itseisarvo — kumpi niistä sitten onkaan suurempi. Murtolukuna numero 10 on sama kuin 10 / 1, joten luvun 10 korkeus on 10. Yksinkertaisin tapa kirjoittaa 10.000017 murtolukuna on 10,000,017 / 1,000,000. Tämän perusteella sen korkeus on 10 miljoonaa. On myös muita tapoja mitata korkeutta (tämä osoittautui suurimmaksi haasteeksi todistuksen esittäjillä).

André-Oortin konjektuurin todistamiseksi Pilan tarvitsi osoittaa, että Shimuran olomuodon sisällä elävällä ei-Shimuran olomuodolla ei ole montaa erikoispistettä. Korkeus on työkalu, joka on tässä avuksi.

Tarkastellaan rationaalilukuja, joiden korkeus on enintään 2. Vaikka on äärettömän monta rationaalilukua, jonka itseisarvo on 2 tai vähemmän, ainoastaan seitsemän niistä on tarpeeksi yksinkertainen jotta sen korkeus on 2 tai vähemmän: 0, 1, 12, 2, tai näiden negatiivit. Yleisesti ottaen, jos voit osoittaa, että rationaalilukujen joukolla on rajallinen määrä korkeuksia, olet osoittanut että joukolla on rajallinen määrä alkioita.

Tällä tavoin korkeus on varsin erilainen itseisarvoon verrattuna. Pila käytti hyödyksi tätä eroa identifioimalla jokaisen erikoispisteen Shimuran olomuodolla, joka on eri reaaliluku. Sitten hän osoitti, että nämä reaaliluvut eivät olleet liian monimutkaisia — niiden korkeudet eivät voineet olla liian suuria. Se tarkoitti, että tiettyyn erikoispisteeseen liittyi äärellisen monta reaalilukua. Koska jokainen erikoispiste vastasi tiettyä reaalilukua, silloin erikoispisteitäkin voisi olla vain rajallinen määrä.

Pilan menetelmä välkysti vältti laskemasta itse Shimuran olomuodon korkeuksia. Sen sijaan hän tutki reaalilukujen korkeuksia ja yhdisti reaaliluvut Shimuran olomuotoon. Mutta tämä strategia toimii vain yksinkertaisille Shimuran olomuodoille.

André-Oortin konjektuurin todistamiseksi kaikille Shimuran olomuodoille, hän ja muut joutuisivat keksimään tavan mitata korkeuksia suoraan.

Universaalit korkeudet

Kun Pila sai aikaan uusia innostavia edistysaskelia André-Oortin konjektuurin parissa, Tsimerman oli edelleen jatko-opiskelijana Princetonin yliopistossa. Hän oli alkanut työstää hänen ohjaajan Peter Sarnakin neuvosta tätä ongelmaa. Pila oli myös ollut Sarnakin oppilas, ja kun hän palasi Princetoniin vuonna 2009 kertomaan uusista löydöksistään, hän ja Tsimerman löysivät toisensa.

“Hän ja minä olemme olleet tämän ongelman parissa siitä lähtien”, Tsimerman sanoo.

Suurin heidän kohtaamansa ohnelma oli monien eri korkeuden mittaamisen tapojen yhteensovittaminen. Esimerkiksi, joskus matemaatikot määrittelevät numeron suuruuden katsomalla sen alkulukutekijöitä itseisarvon sijaan. André-Oortin konjektuurin todistamiseksi heidän piti ensin kääntää jokainen näistä kompleksisuuden määritelmistä Shimuran olomuodolle.

Pila ja Tsimerman saivat aikaan osittaista edistymistä tähän suuntaan. Mutta pidemmälle meneminen vaati aina vain monimutkaisempia matemaattisia ideoita, joita he tunsivat yhä vain huonommin. Erityisesti, heidän piti löytää tapa jolla yhdistää kaikki nämä eri korkeuksien mittaamisen tavat yhdeksi johdonmukaiseksi luvuksi (joka varmistaisi, että he olivat ottaneet huomioon kaikki tavat joilla pisteet saattaisivat erota toisistaan).

Tsimerman tiesi, että Shankarilla oli kokemusta sellaisesta matematiikasta, jota he kaipasivat tämän saavuttamiseksi, ja hän pyysi tätä liittymään mukaan yhteisprojektiin elokuussa 2020. Kolme matemaatikkoa työskentelivät ongelman parissa useita kuukausia, mutta edistys hidastui.

“Joskus vaikutti siltä että me olimme lähellä; joskus vaikutti taas siltä että meillä oli perustavanlaatuisia esteitä, joiden yli piti päästä”, Shankar sanoi. He päättivät ottaa askeleen taaksepäin viime talvena, ajatellen että he voisivat edistää muita juttuja.

Pari kuukautta myöhemmin Shankar esitteli Pilalle ja Tsimermanille Toronton yliopiston Michael Groechenigin ja Free University of Berlinin Hélène Esnaultin työtä hänen puhuttuaan Groechenigin kanssa. Hän epäili, että heidän tuloksensa — plus Gal Binyaminin ja muiden tekemä työ — voisi auttaa heitä todistamaan, että kaikki eri korkeuden käsitteet sulautuvat yhteen tavalla, jota he tarvitsivat.

Tuo vainu osoittautui oikeaksi, kun Esnault ja Groechenig olivat täydentäneet aiempaa työtään. Pila, Shankar ja Tsimerman sitten käyttivät heidän laajennettua työtään todistamaan, että erikoispisteiden korkeudet eivät koskaan kasva liian suuriksi millekään Shimuran olomuodolle. Tämän myötä André-Oortin konjektuurin lopullinen todistus oli lähellä.

“Jossain mielessä koko tutkielman pointti oli selvä, jo joskus puolitoista vuotta sitten, mutta sen saamiseksi toimimaan vaadittiin, että kehitettiin tällaisia monimutkaisia koneen osasia, joiden yhteensovittaminen vei paljon aikaa”, Tsimerman sanoo.

Pila, Shankar ja Tsimerman lopulta syksyllä 2021 julkaisivat tuloksensa. He osoittivat, että millään Shimuran olomuodon sisällä elävällä olomuodolla ei voi olla liian montaa erikoispistettä ilman, että kyseessä on itsessään Shimuran olomuoto.

Vaikka tutkielman lukeminen ja varmistaminen huolellisesti ottaa aikansa, matemaatikot ovat jo pohtimassa sen vaikutuksia. Jos tutkielman ideoita voidaan soveltaa laajemmin, he saattaisivat esimerkiksi laajentaa tulosta 1980-luvulta ongelmaan nimeltä Mordellin konjektuuri — ja tämä saisi aikaan numeroteorian uusien löydösten vyöryn.

“Tämä on läpimurto, selvästikin läpimurto”, Liu sanoo.

Artikkelin julkaissut Quanta Magazine

Tiede

Eulerin 36 upseerin pulmalla on kvanttiratkaisu

29 tammikuun, 2022 paatoimittaja Kommentoi

kirjoittanut Inés Urdaneta

Mikä on tämä 240 vuotta vanha pulma?

Leonhard Euler (1707 – 1783), sveitsiläinen matemaatikko ja fyysikko, tunnetaan ehkä eniten hänen kompleksilukuja kuvaavasta Eulerin yhtälöstään: e^iφ + 1 = 0.

Geometric interpretation of Euler's identity, where i represents the imaginary axis of the complex plane and φ is the angle. — *Eulerin yhtälön geometrinen kuvaus, jossa i on imaginääriakseli kompleksitasolla ja φ on vaihekulma.*

Eulerin panos matematiikkaan on kiistämätön fysiikassa, erityisesti kvanttimekaniikassa. Nyt Eulerin pulmalle on löytynyt ratkaisu, joka todennäköisesti vaikuttaa asioihin kvanttilaskennassa ja informaatioteoriassa.

Eulerin 36 upseerin pulma on seuraavanlainen:

Valitaan kuudesta eri rykmentistä kuusi upseeria kuudella eri sotilasarvolla. Halutaan järjestää nämä yhteensä 36 upseeria paraatiin 6x6 -neliömuodostelmaan siten, että jokaisessa rivissä ja jokaisessa jonossa on edustettuna kaikki kuusi rykmenttiä ja sotilasarvoa. Siis siten, että jokaisessa rivissä ja jokaisessa jonossa olisi yksi upseeri kutakin sotilasarvoa kustakin rykmentistä. Onko tämä mahdollista?

Euler yritti vuonna 1779 järjestää upseereita pyydetyllä tavalla, mutta ei onnistunut siinä, ja arvasi lopulta tehtävän olevan mahdoton. Itseasiassa Euler otaksui vastaavanlaisen neliön muodostamisen olevan mahdotonta kaikilla muotoa 2 + 4k (k = 1, 2, 3, …), olevilla määrillä rykmenttejä ja sotilasarvoja. Hän muotoilikin siitä nk. Eulerin konjektuurin, jota ei kuitenkaan kyennyt todistamaan [6].

Esimerkiksi hypoteettisessa neljän ulottuvuuden tilanteessa (d=4, neljä kategoriaa ja 4 alakategoriaa), jossa kategoriat ovat esineen muoto (neliö, ympyrä, kolmio ja tähti), ja alakategoriat ovat värejä (sininen, vihreä, punainen ja keltainen), ratkaisu jossa mikään väri tai muoto ei toistu missään rivissä tai sarakkeessa, ja jossa lisäksi jokainen muoto on eri värinen, on esitetty alla:

Tämä ehto ei täyty diagonaaleilla, ja kiinnostavaa kyllä kaksi päädiagonaalia 6×6 neliöstä toistavat molemmat muodon (kaikki 4 paikkaa on neliöiden täyttämiä yhdellä päädiagonaalilla ja tähtien leikkaavalla diagonaalilla). Ja koska molemmat päädiagonaalit sisältävät samoja muotoja, värit eivät toistu diagonaalilla. Sanomme, että tämä ratkaisu johtaa ”diagonalisaatioon”.

Euler havaitsi, että sellainen järjestely oli mahdoton, kun d=6. Vasta paljon myöhemmin, vuonna 1960, tietokoneiden avulla, matemaatikot osoittivat että ratkaisu on olemassa mille tahansa kahta suuremmalle määrälle sotilasarvoja ja rykmenttejä, paitsi kuudelle.

Kuietnkin kvanttifyysikoiden ryhmä Intiasta ja Puolasta on osoittanut, että ratkaisemattoman pulman vastaavalla kvanttimaailman analogilla on analyyttinen ratkaisu. Heidän tutkimuksensa nimi on ”Thirty-six entangled officers of Euler: Quantum solution to a classically impossible problem”, joka on annettu vertaisarvioitavaksi Physical Review Lettersiin, fysiikan huippujulkaisuun.

Tämä löydös vaatii algoritmien käyttämistä, joilla on kvanttiominaisuuksia, erityisesti kvanttitilojen superpositio. Tilojen superpositio esimerkiksi tarkoittaisi tässä tapauksessa tietyn sotilasarvon ja tietyn rykmentin yhdistelmää jokaiselle upseerille. Tai geometristen muotojen ja värien tapauksessa kvanttiupseeri olisi tila, joka koostuu esimerkiksi sinisestä neliöstä ja keltaisesta tähdestä, joille on molemmille annettu painokertoimet, jotka ilmaisevat suhteellisen esiintyvyyden kullekin kategorialle. Sellaisia painokertoimia kutsutaan amplitudeiksi.

Algoritmi muodostaa mahdolliset kombinaatiot ja laskee amplitudit, kunnes algoritmi on konvergoitunut, jolloin se on näyttänyt kaikki mahdolliset yhdistelmät. Tulokset olivat hämmentäviä kahdesta syystä. Ensinnäkin, koska löydetty ratkaisu käytti tiloja, jotka olivat kvanttikietoutuneet toisiinsa (eli että niitä ei voida hajottaa eri kategorioiksi), ja kvanttikietoutumisen määrä oli maksimissaan, ominaisuus joka on erittäin vaikeaa saavuttaa kvanttitiloilla. Toisin sanoen, työkalu teki mahdolliseksi löytää maksimaalisen kietoutuneita kvanttitiloja erittäin systemaattisella tavalla. Kvanttikietoutuminen on olennainen piirre kvanttilaskennassa, sillä se suojaa kvanttitiloja korruptoitumiselta. Näin maksimaalisen kvanttikietoutuneet tilat ovat paras suoja mikä kvanttitiloilla voi olla.

Toiseksi, tutkijat saivat selville, että kultainen leikkaus määrittää kaikki amplitudit, joita maksimaalisen kietoutuneessa ratkaisussa esiintyy, minkä takia tila sai nimen kultaisen maksimaalisen kietoutuneisuuden amplituditila.

”Kiinnostavaa kyllä, algoritmin tuottamien kertoimien välinen suhde oli Φ, eli 1.618…, kuuluisa kultainen leikkaus.” Daniel Garisto, Quanta Magazine

Ratkaisun/kietoutuneisuuden visualisoimiseksi Eulerin kvanttiupseereilla, me voimme tarkastella allaolevaa kuviota. Jokaisen upseerin sijainti, i:nnes rivi ja j:nnes sarake, on esitetty vastaavalla rivillä ja sarakkeella matriisissa. Upseerien sotilasarvot ja rykmentit on esitetty korttien muodossa vastaavina numeroarvoina ja maina. Jokaisen upseerin sotilasarvo on superpositiossa kahden sotilasarvon ja kahden rykmentin kanssa. Jokaisen kortin arvon kirjain vastaa siihen liittyvän elementin amplitudin suuruutta. Klassinen Eulerin pulman ratkaisu vastaisi matriisia, jossa jokaisessa matriisin alkion paikassa on vain yksi kortti.

^{Ratkaisun/kvanttikietoutumisen visualisointi Eulerin kvanttiupseereilla. Kuva otettu tutkielmasta.}

Me havaitsemme, että matriisiin syntyy struktuureja, esimerkiksi, ässät ovat kietoutuneet kuninkaiden kanssa, koska ne esiintyvät ainoastaan kuninkaiden seurassa, kuningattaret jätkien kanssa, kympit pelkästään 9ien kanssa. Eli, ne ovat ainoastaan ja aina kietoutuneet niiden välittömään naapuriin. Lisäksi, korttien värit eivät ole kietoutuneet toisiinsa. Näin upseerit ryhmitellään yhdeksään nelielementtiseen joukkoon, joista jokaisessa on samat värit ja lukuparit.

Tämä tulos on merkittävä, sillä se tarkoittaa että ratkaisussa esiintyy maksimaalinen kietoutuminen.

Ratkaisulla on myös muita hienoja ominaisuuksia, kuten kultaisen leikkauksen esiintyminen (1,618….). Nassim Harameinin tulevassa tutkielmassa otsikolla ”Skaalainvariantti kenttien, voimien ja hiukkasten yhtenäistäminen kvanttivakuumiplasmassa” näytetään miten kultainen leikkaus syntyy myös Harameinin yleistetyssä holografisessa mallissa. Tämä työ tulee käyttöön moduulissa 8, ”Universaali skaalautuvuuden laki”, ja kun se on julkaistu, me kykenemme syventymään enemmän tämän amplitudien kultaisen leikkauksen ratkaisuun ja puhumaan lisää sen vaikutuksista.

Artikkelin julkaissut Resonance Science

Kehitä intuitiota ennen siihen luottamista

Opiskele todistuksia

Konseptien opiskelu

Todista se itse

Matematiikan ulkopuolella

Mikä on todistus?

Mitä on matematiikka?

Mikä on propositio?

Mikä on todistus?

Mikä on lause?

Opi formaalin logiikan perusteet

Boolen algebra

Todistus: Sateessa kävely

Muita Boolen algebraan liittyviä asioita

Kvanttorit ja joukko-opin perusteita

Propositiot matematiikassa

Päättelysäännöt

Tunne keskeiset todistusmenetelmät

Suora todistus

Todistus: Ei ole olemassa suurinta mahdollista luonnollista lukua

Ääretön totuustaulukko?

Todistus: Pythagoraan lause

Kontrapositiiviset todistukset

Todistus: Neliöt ja parilliset luvut

Todistus vastaväittämällä

Todistus: Irrationaaliluvuissa toistuu ainakin yksi numero äärettömän monta kertaa

Kyyhkyslakkaperiaate

Matemaattinen induktio

Todistus: Ensimmäisen N parittoman luvun summa

Todistus: Aritmetiikan peruslause (vahva induktio)

Joukkoonkuuluvuusperiaate

Todistus: Aritmetiikan peruslause

Todistus: kahden neliöjuuren irrationaalisuus

Milloin käyttää mitäkin todistusmenetelmää

Muuta pulmaa

Etsi invariantteja ominaisuuksia

Todistus: Conwayn sotilaat

Todistus: Punaiset, valkoiset ja vihreät pallot

Satunnaisia vinkkejä

Lisälukemista

Pulma 1: Ositus

Pulma 2: Unioni

Pulma 3: Yhdessäolo

Harjoituksia

Erilaiset olomuodot

Erikoispisteet

Pilan edistys

Universaalit korkeudet

Eksopolitiikka, UFOt, Paranormaalit ilmiöt, Tietoisuus