Chas Blakemore
10. joulukuuta 2017
Kurssityö kurssille PH240, Stanfordin yliopisto, syksy 2017
Johdanto
Stargate Atlantiksen ja Marvel-sarjakuvien Realm of Kingsin fiktiivisestä maailmasta NASAn Eagleworks Propulsiolaboratorioon, nollapiste-energiaa, jota kutsutaan myös vakuumienergiaksi, pidetään potentiaalisesti rajattomana ja kaikkialla läsnäolevana energianlähteenä, jos löydetään vain keino ottaa se käyttöön. [1] Nollapiste-energia voidaan kuvata eri tavoin, mutta sen perusmuodossaan se on minimaalinen, mutta nollasta poikkeava kvanttimekaanisen systeemin energia. Kvanttikenttäteoriassa nollapiste-energia voidaan laskea nollafotonimoodin odotusarvoisena energiana. [2] Systeemissä, jossa ei ole fyysisiä rajoja, odotusarvoinen nollafotonimoodin energia eroaa nollasta! Ja kuitenkin, jos tämä energia on kaikkialla avaruus-ajassa läsnä, sitä ei pystytä suoraan havaitsemaan.
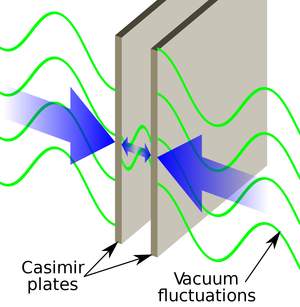 |
| Kuva 1: Voima, joka syntyy vakuumitilojen välisistä eroista, ja näin reunoille vaikuttaa paine. (Lähde: Wikimedia Commons) |
Konseptuaalinen viitekehys
Pedagogisista syistä tarkastelemme nollapiste-energian populaaria muotoilua. Kaikkein kiinnostavin ja relevantein viitekehys nollapiste-energialle voidaan ymmärtää kvanttielektrodynamiikan, fotonien ja elektronien kvanttikenttäteorian, avulla. Kaunistelemalla poikkeuksellista matemaattista ja konseptuaalista taustaa, kvanttikenttäteoriassa tilaenergia lasketaan Hamiltonin operaattorin. <H>, odotusarvona, joka kuvaa energiatilaa operaattorien avulla, joita sovelletaan aaltofunktioon. Lopullinen lasku yleensä vaatii tilassa olevien partikkelien liikemäärämomenttien yli integrointia.
Schwartzia mukaillen, me voimme laskea nollafotonivakuumitilan energian, jolla on äärettömät rajat, systeemi joka ei ole millään tavalla fysikaalinen, realisoitavissa tai kuvaukseltaan täydellinen, mutta yhtä kaikki pedagoginen. [2] Jälleen kaunistelemalla paljon matemaattista taustatietoa (jota myös rohkaisemme kiinnostuneen lukijan tutkimaan viitteestä [2]), huomaamme, että
Evac = <H> ∝ ∫ k3 dk → ∞.
Ja näin me voimme nähdä, että vakuumitilan odotusarvoinen energia divergoi! Tottakai tämä ei ole oikea fysikaalinen systeemi, sillä mitään hiukkasia ei ole läsnä, eikä ole myöskään rajoja, mutta se kuvaa ideaa tyhjässä avaruudessa läsnä olevasta energiasta.
Hollantilainen fyysikko Hendrik Casimir vei tämän formalismin pidemmälle ja tutki hieman fysikaalisempaa systeemiä vakuumissa, joka koostuu ontosta ja johtavasta kuutiosta, jonka sivun pituus on L. [3] Kuution vieressä on neliön muotoinen johtava sivulevy, jonka pituus on L, yhdensuuntaisesti ja asetettu lähelle yhtä kuution sivua. Sitten hän laski kaksi energiaa: nollafotonitilan energian, eli sähkömagneettisen vakuumitilan energian, alueella joka on rajoitettu kahden toisiaan lähellä olevan tason väliin; sekä vakuumitilan energian muualla kuutiossa. Kaksi suuretta eroavat toisistaan, sillä rajoitusehdot sallivat ainoastaan tietyt moodit, eli seisovat aallot, kummassakaan alueessa.
Muodollisesti molemmat energiat divergoivat, mutta ero näiden kahden lausekkeen välillä on hyvin määritelty, ja sitä voidaan manipuloida voimien laskemiseksi. Casimir tulkitsi tämän interaktiona kahde toisiaan lähellä olevan levyn välillä, ja sai selville, että siinä esiintyy vetovoima, joka pienenee nopeasti levyjen välimatkan kasvaessa. Kahden levyn poikkileikkausgeometria ja siitä seuraava voima kuvataan kuvassa 1, jossa voima on ilmaistu varsin yksinkertaisella kaavalla F = (π2ℏc/240a4) L2 jollekin etäisyydelle a. Vaikka vaikutus on poikkeuksellisen pieni, hän ennusti, että ”kokeellinen vahvistus ei vaikuta mahdottomalta, ja se saattaisi olla jossain määrin kiinnostavaa”. [3]
Tässä laskennassa ei ole otettu mukaan useita merkittäviä muita asioita, kuten Casimirin laatikon metallien fyysisiä ominaisuuksia. Kuitenkin eri materiaalit, joko metallit tai epämetallit, yksinkertaisesti muuttavat lasketun voiman suuruutta, kun taas riippuvuus etäisyydestä ja pinta-alasta säilyy samana.
Kokeellinen vahvistaminen
Olemme nähneet, että on olemassa järkevä teoreettinen viitekehys energialle, joka liittyy sähkömagneettisiin vakuumitiloihin, ja että elektrodien tietyillä geometrioilla voidaan saada epäsuorasti keino havaita näitä vakuumienergioita. Voitaisiin kysyä, onko sellaista vahvistettu kokeellisesti. Vaikka vuonna 1958 M. J. Sparnaay teki mittauksen, hän sai ainoastaan selville, että hänen mittauksensa eivät olleet Casimirin ennusteen kanssa ristiriidassa, ja että ne olivat todella kaukana tarkoista lukemista. [4]
Tuoreemmalti vuonna 1997, Washingtonin yliopiston fyysikko käytti torsioheiluria mittaamaan kahden johtimen välistä voimaa: yksi levymäinen ja toinen puolipallon muotoinen. [5] Hän sai selville, että alle 1 mikronin etäisyyksillä, kahden levyn välillä oli verrattain merkittävä voima, jota ei voitu selittää Casimirin ennustamalla interaktiolla. Hän otti huomioon muutokset voimaan geometrian eroista, oikeiden metallien rajallisen johtavuuden sekä lämpö- ja sähköstaattiset taustavaikutukset. Tämä oli ensimmäinen suora havainto ja tilastollisesti eheä analyysi, jolla vahvistettiin voima, jonka Casimir oli postuloinut melkein 50 vuotta sitä ennen.
Vuodesta 1997 eteenpäin on ollut useita kokeita, jotka ovat tarkastelleet hienovaraisempia Casimirin ilmiön yksityiskohtia, sekä tutkimuksia, joissa on havainnoitu muita vakuumienergiaan liittyviä ilmiöitä, joita usein kutsutaan alkuperäisen Casimir-ilmiön korollaareiksi. Aiheesta kiinnostunut lukija voi tutkia plasmamallia vs. Drude-mallia eli dynaamista Casimir-ilmiötä.
Lopullinen tavoite: työntövoima ilman polttoainetta
Kahden metallilevyn välillä olevan voiman mittaaminen on ihan ookoo (itse asiassa poikkeuksellista), mutta pragmaatikot ihmettelevät mitä käyttöä tällä mittauksella on, mihin sitä edes voitaisiin soveltaa. Tällaisessa ajattelussa me palaamme ensimmäiseen viitteeseemme: väitettyyn ”Casimirin raketin” työntövoimaan, jota tutkittiin NASAn Eagleworks-laboratoriossa. [1] Tutkimalla suhteellisen uutta kvanttivakuumifluktuaatioiden havaittavaa maailmaa, ja käyttämällä avaruusinsinöörejä, NASA toivoo rakentavansa työntövoimajärjestelmän, joka ei vaadi polttoainetta, ainoastaan sähkövoiman muodossa olevaa energiaa.
 |
| Kuva. 2: Valokuva työntömoottorin ontelosta (kuparinen, vasemmalla), sen tukirakenteesta ja vakuumikammiosta, joka sitä ympäröi (taustalla). (Kuva: Wikimedia Commons) |
Rakettien työntövoimaksi käytettäessä, nykyiset avaruusteknologiat riippuvat melkein täysin kemikaalien käytöstä polttoaineina, mm. nestemäinen happi, hydratsiini, kiinteät komposiittipolttoaineet ja paljon muuta. Kaikkein merkittävin haittapuoli sellaiselle polttoaineelle on kiinteä työntövoima suhteessa painoon. Jos haluaa enemmän työntövoimaa, tai pidempiä aikoja, silloin pitää tuoda enemmän polttoainetta. Olisi paljon kivempaa, jos voisi tuoda aurinkovoimakäyttöisen avaruusmoottorin, kiinteäpainoisen, ja antaa sen työntää avaruusalusta. Mutta mikä voisi tarjota työntövoimaa?
NASAn vastaus: kvanttivakuumifluktuaatiot. Ja näin Eagleworks sai alkunsa. Heidän tarkoituksensa on käyttää monimutkaisia ja erittäin erityislaatuisia johtavia onteloita generoimaan työntövoimaa, joka ”puskee” avaruuden vakuumia vastaan ohjaamalla virtuaalista elektronien ja positronien virtaa, jota syntyy seisovista radiotaajuuksisista aalloista, jotka ovat suljetussa ontelossa. Jos tämä on mahdollista, ainoa mitä tarvittaisiin on hieman sähköä ja silloin ainoa ihmiskunnan este päästä tähtiin olisi sinne matkaamiseen kuluva aika.
Eagleworks on julkaissut paperin, jossa kuvataan oletettu ja ylenpalttisen kiistanalainen mitattu työntövoima, jota syntyy sähkömagneettimoottorin (EM) prototyypistä kuvassa 2. [1] Heidän alkuvaiheen koetta vuonna 2014 ei tehty vakuumissa, mikä sai useat vastaväittäjät esittämään, että työntövoima johtui todennäköisesti lämpösiirtymästä, joka indusoitui sähkömagneettikentästä. Tuoreessa julkaisussa on tarkempi mittaus, joka on suoritettu vakuumissa, joka voi olla paljon ratkaisevampi. Suuren vuoden 2011 Superluminaalisen Kuumotuksen jälkeen, NASAn tulokset vaativat äärimmäisen tarkkaa syynäystä, ja jos mahdollista, kokeen toistamista.
Vastalauseet
Kuten aiemmin mainittua, tällä työntövoiman mittauksella, joka syntyy avaruusajan vakuumia vasten puskemisesta, on paljon vihamiehiä fyysikoiden yhteisössä, ja ihan aiheesta. Kaikkein ilmiselvin ongelma on liikemäärän säilymislain rikkominen. NASA on väittänyt rakentaneensa ”työntömoottorin”, joka ainakin teoriassa voi työntää itsensä lepotilasta ilman, että se sylkee ulos ainetta tai fotoneja. Triviaalisti ploppu ≠ palku joka on ongelma! On mahdollista, vaikkakin epätodennäköistä, että moottori tuottaa työntövoimaa sylkemällä jotain toisen tyyppisiä heikosti vaikuttavia hiukkasia, ehkä jopa mekanismilla, jota nykyhetken standardimalli ei edes tunnista.
Kaikki fysiikan argumentit sikseen, mittaus väitti oletettavasti havainneen kymmenien mikronewtoneiden työntövoiman ja hitaan (1/f) ajelehtimisen kertaluokkaa satoja mikronewtoneita. [1] Puhtaan mittateknisestä katsantokannasta tämän tyyppinen mittaaminen on täynnä virhettä, vaikka käytettäisiin tekniikoita, joilla signaali identifioitaisiin spektrin ominaisuuksista. Ajan mittaan on mahdollista mitata paremmin.
Johtopäätökset
Energian ja työntövoiman kerääminen avaruuden tyhjiöstä voi olla kiistämättä hämmästyttävää, ja se on NASAn Eagleworks-laboratorion päätavoite. Sellaisen idean tulee noudattaa fysiikan lakeja kuten yksinkertainen liikemäärän säilyminen, ja olisi hyvä, jos se on tarkasti kuvattu mekanismi, vaikka se olisi pelkkä kuvaus.
Vuonna 2017, vakuumifluktuaatioiden on väitetysti osoitettu tarjoavan EM-prototyyppimoottorille työntövoimaa. Tämä posketon mittaus on tyypillisesti mahdoton, sekä fundamentaalisten argumenttien että mittateoreettisen katsantokannan näkökulmasta, niinkuin yllä esitetty lyhyt käsittely osoitti.
© Chas Blakemore. The author warrants that the work is the author’s own and that Stanford University provided no input other than typesetting and referencing guidelines. The author grants permission to copy, distribute and display this work in unaltered form, with attribution to the author, for noncommercial purposes only. All other rights, including commercial rights, are reserved to the author.
Lähdeviitteet
[1] H. White et al., ”Measurement of Impulsive Thrust from a Closed Radio-Frequency Cavity in Vacuum,” J. Propul. Power 33, 830 (2017).
[2] M. D. Schwartz, Quantum Field Theory and The Standard Model (Cambridge University Press, 2013).
[3] H. B. G. Casimir, ”On the Attraction Between Two Perfectly Conducting Plates,” Kon. Ned. Akad. Wetensch. Proc. 51, 793 (1948).
[4] M. J. Sparnaay, ”Measurements of the Attractive Forces Between Flat Plates,” Physica 24, 751 (1958).
[5] S. K. Lamoreaux, ”Demonstration of the Casimir Force in the 0.6 to 6 μm Range,” Phys. Rev. Lett. 78, 5 (1997).
Artikkelin julkaissut stanford.edu