Kirjoittanut Joseph Mellor
Matemaatikoksi tuleminen tapahtuu kolmen vaiheen kautta: aritmetiikka, algebra ja argumentit (eli todistukset). Useimmat ihmiset oppivat aritmetiikan ja algebran, mutta riippuen urapoluista, he harvoin opettelevat matemaattisen todistamisen taidon. Jopa valinnaisena aiheena opiskeltuna todistukset ovat pelottavia. Opiskelijat käyttävät vuosia oppimaan miten ratkaista ongelmia seuraamalla tiettyjä askelia, ja sitten kaikki tuntuu yhtäkkiä muuttuvan. Derivaatan ketjusäännöillä laskemisen sijaan, nyt täytyykin yhtäkkiä osoittaa, että 2:n neliöjuuri on irrationaalinen. Jos et osaa ratkaisua ulkoa, mistä edes aloittaa?
Tässä artikkelissa haluan antaa joitain ohjeita miten todistaa lauseita matematiikassa samaan tyyliin kuin fysiikan artikkeleissani. Ensimmäinen osio liittyy yleisiin ohjeisiin, keskiosassa käsitellään todistustekniikoita ja loppuosassa puhutaan tempuista, joita voi soveltaa tietynlaisiin ongelmiin. Laitan myös linkkejä oppimateriaaleihin pitääkseni artikkelin lyhyenä ja antaakseni käsityksen useamman tyylisistä todistuksista. Käyn myös perusasiat läpi, mutta voit hyvin hypätä jonkun kohdan yli jos siltä tuntuu.
Kehitä intuitiota ennen siihen luottamista
“Jos ihmiset tietäisivät miten kovasti näin vaivaa päästäkseni tälle tasolle, se ei tuntuisi yhtään hienolta.”
— Michelangelo
Monissa maissa on tietynlaisen “matikkapersoonan” käsite. Jokaisella on oma määritelmänsä “matikkapersoonalle”, mutta yleinen idea on, että jotkut ihmiset ovat syntyneet hyvien matematiikan taitojen kanssa. Sellaisia ihmisiä ei ole oikeasti olemassa. Voi vaikuttaa siltä, että “matikkapersoonat” näkevät ongelman ja tietävät heti miten ratkaista sen, mutta se johtuu vain siitä, että he ovat aiemmin ratkaisseet sen tai ovat nähneet jonkun toisen ratkaisevan senkaltaisia pulmia. Uuden pulman kanssa he käyttävät usein tekniikoita, joita he ovat oppineet, muuntamaan pulman sellaiseen muotoon, että he saavat siitä oivalluksia. Se on heidän intuitionsa. Miten siis voit kehittää intuitiota?
Opiskele todistuksia
Todistuksien katseleminen on helppoa, mutta niiden opiskelu on vaikeampaa. Todistukset usein sivuuttavat sen miten sen keksijä alunperin idean sai päähänsä. Sinulle tämä tarkoittaa, että sinun tulisi kysyä itseltäsi miksi kukaan tekisi asian siten kuin matemaatikko sen teki. Saatat ehkä jopa haluta kokeilla jotain erilaista ja katsoa miksi se ei toimi (jos se toimii, silloin olet keksinyt uuden todistuksen). Vaihtoehtoisesti, yritä etsiä samankaltainen todistus tai todistus samankaltaisesta ongelmasta ja katso onko tuon todistuksen ymmärtäminen avuksi alkuperäisen todistuksen ymmärtämisessä.
Infoaikana hyvien todistusten etsiminen on joko verkkolähteiden etsimistä tai oppikirjojen kahlaamista. Jos et tiedä mistä aloittaa, julkaisin artikkelin, jossa on linkkejä moniin relevantteihin lähteisiin. Linkkaan myös todistuskohtaisia lähteitä tähän artikkeliin. Voit etsiä asiaan vihkiytyneiltä foorumeilta suosituksia kirjoille. Jos olet kiinnostunut tietystä aiheesta, etsi aiheesta kurssi minkä tahansa yliopiston sivulta, tutki esitietovaatimuksia ja etsi niistä kursseja.
Konseptien opiskelu
Todistuksia opiskellessa tulisi opiskella myös eri matematiikan alojen konsepteja. Se antaa paremman ymmärryksen, jota tarvitaan erilaisten todistusten ymmärtämiseksi, ja jokainen opittu konsepti on työkalu työkalupakissa. Jos haluat esimerkiksi todistaa, että Rubikin kuutio on mahdollista ratkaista alle 30 siirrolla, ilman ryhmäteoriaa olet umpikujassa. Lisäksi monet matematiikan osa-alueet ovat päällekkäin toistensa kanssa, jolloin tietoisuuden laajentaminen auttaa monin eri tavoin.
Todista se itse
Viimeisenä, yritä itse todistaa asioita. Tässä kohtaa aiemman otsikon ”ennen siihen luottamista” tulee mukaan kuvioon. Olen nähnyt opiskelijoiden aloittavan oikealla idealla ja hylkäävän sen ennenaikaisesti, koska he eivät usko sen toimivan. Sen sijaan suosittelisin, että jos et usko jonkin idean toimivan, katso miten pitkälle voit idean kanssa mennä. Useimmissa tapauksissa sattuu yksi seuraavista:
- Idea toimii ja todistus on valmis.
- Idea toimii joissain erikoistapauksissa.
- Osoittautuu, ettei idea toimi, mutta se luo perustan paremmalle idealle.
- Osoittautuu, ettei idea toimi, mutta sait harjoitusta todistaessasi ettei idea toimi.
Kokemuksen karttuessa sinulla on parempi ymmärrys mitkä ideat toimivat ja haaskaat vähemmän aikaa. Lisäbonuksena nihkeä tunne siitä, että luulet todistaneesi jotain mutta et edelleenkään ole varma onnistuitko, katoaa.
Matematiikan ulkopuolella
Voit soveltaa tässä esitettyä melkein mihin tahansa tehtävään, joka ei vaadi fyysistä voimaa. Todennäköisesti minkä tahansa matematiikkaan liittyvän termin voisi korvata shakkiin liittyvällä termillä ja voisi laittaa Daniel Naroditskyn (shakin mestari ja opettaja Youtubessa ja Twitchissa) videolle siitä puhumaan ja kukaan ei huomaisi mitään eroa.
Mikä on todistus?
Jotta ymmärtäisi mikä tekee todistuksesta todistuksen, pitää ymmärtää ensin muutama määritelmä.
Mitä on matematiikka?
Matematiikkaa kuvataan yleensä sen osa-alueiden, kuten joukko-opin, algebran, laskennan, funktionaalianalyysin jne., muodostamana kokonaisuutena, mutta tämä määritelmä ei ole hyödyllinen ihmisille, jotka eivät jo ymmärrä muutamia näistä osa-alueista. Sen sijaan haluan määritellä matematiikan joukoksi määritelmiä (eli aksioomia) ja sääntöjä (eli logiikkaa). Siinä kaikki. Saattaa kuulostaa siltä, että vähättelen matematiikkaa, mutta älä pidä yleisyyttä heikkoutena. Kaikki, mikä voidaan kuvata määrittelyjen ja sääntöjen avulla, voidaan kuvata matematiikan tai logiikan avulla.
Mikä on propositio?
Propositio on väittämä, joka voi olla joko tosi tai epätosi. ”Kaksi plus kaksi on neljä.” on tosi väite, ”Kaksi plus kaksi on viisi.” on väärä väite, eikä ”Väritön vihreä nukkuu raivokkaasti.” eikä ”Mikä on aurinko?” ole väite. Monimutkaisempi propositio olisi jotain Heine-Cantorin lauseen kaltaista, jossa sanotaan: ”Jokainen jatkuva funktio kompaktilla välillä on tasaisen jatkuva”.
Mikä on todistus?
Todistus on matemaattisten toteamusten ketju, joka selvittää onko jokin propositio tosi vai epätosi. Nämä matemaattiset toteamukset tulee aloittaa määritelmillä ja niiden tulee seurata logiikan sääntöjä. Yleisesti todistukset näyttävät tältä:
- Määritelmän mukaan, voimme todeta A.
- Loogisen säännön X mukaan, kun otetaan huomioon A, voimme todeta B.
- Loogisen säännön Y mukaan, kun otetaan huomioon B, olemme osoittaneet proposition S epä/todeksi.
Jos pidät matematiikkaa pelinä, jossa on omat säännöt ja pelinappulat (eli siis muodollisuutensa), voit pitää todistusta kuin sarjana siirtoja pelissä.
Mikä on lause?
Lause on todistuksen tulos. Aivan kuten on mahdollista käyttää toisten kirjoittamaa koodia oman kirjaston kirjoittamiseen, voit käyttää toisten työtä todistuksen kirjoittamiseen. Esimerkiksi, voin osoittaa, että x² välillä [0, 1] on tasaisesti jatkuva osoittamalla, että se on jatkuva ja että [0, 1] on suljettu väli. Sitten lainaan Heine-Cantor -lausetta ja olen valmis.
Opi formaalin logiikan perusteet
“Sitä paitsi on virhe uskoa, että täsmällisyys on yksinkertaisuuden vihollinen. Päinvastoin, lukuisat esimerkit vahvistavat, että täsmällinen menetelmä on samalla yksinkertaisempi ja helpommin ymmärrettävä. Juuri pyrkimys täsmällisyyteen pakottaa meidät etsimään yksinkertaisempia todistusmenetelmiä.”
— David Hilbert
Saatat lukea tätä kappaletta ja miettiä ”eikö tuo sano samaa kuin artikkelin otsikko”. Ei. Formaali logiikka koostuu joukosta määritelmiä ja sääntöjä, jotka muodostavat useimpien argumenttien pohjan. Tämä osuus tulee olemaan pitkä, mutta käsittelen suurimman osan siitä mitä tietoja tarvitset.
Boolen algebra
Otetaan väittämä ”Jos henkilö kävelee sateessa tai hyppää altaaseen, hän kastuu.” Jättäen huomiotta sadevaatteet ja sateenvarjot, miten voisit esittää, että tämä väittämä on totta? Vaikka me menemme seuraavassa osiossa todistustekniikoihin, nämä tekniikat ovat oikopolkuja totuustauluun, taulukkoon joka ottaa jokaisen mainitun väittämän totuusarvon ja tarkastelee mitä tapahtuu kun niiden totuusarvo on joko totta tai epätotta. Proposition osoittamiseksi me näytämme, että väitteen sarake taulussa on aina totta.
Todistus: Sateessa kävely
Meidän tapauksessamme meillä on kaksi syötelausetta:
- Henkilö kävelee sateessa.
- Henkilö hyppää altaaseen.
Ja kolme tuloslausetta:
- Henkilö kastuu.
- (Henkilö kävelee sateessa) TAI (henkilö hyppää altaaseen).
- JOS ((henkilö kävelee sateessa) TAI (henkilö hyppää altaaseen)), SILLOIN (henkilö kastuu).
Olen lisännyt sulkeita, jotta voit nähdä miten lauseet rakentuvat yhdistelemällä yksinkertaisempia. Totuustaulun koostamiseksi tarkastelemme mitä tapahtuu, kun me asetamme jokaisen syötelauseen joko todeksi tai epätodeksi ja sitten käytämme formaalilogiikan sääntöjä (eli Boolen algebraa) täyttämään totuustaulun loppuun.
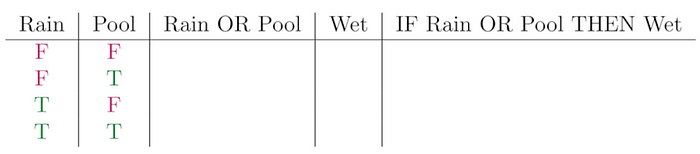
Meidän tulee tietää totuustaulut x TAI y:lle sekä JOS x NIIN y:lle, jotka näkyvät alla.

x TAI y on totta jos x on tosi, y on tosi tai molemmat ovat totta. Väittämässä JOS x NIIN y x:ää kutsutaanedeltäjäksi ja y:ä seuraamukseksi. Me voimme täyttää yhden sarakkeen lisää taulussa.

Samoin, JOS x NIIN y on tosi, kun x on epätosi tai molemmat x ja y ovat tosia. Tämä totuustaulu tulisi olla järkeenkäypä: Jos esimerkiksi meillä on väittämä ”jos kävelet sateessa, silloin kastut”; jos olet kävellyt sateessa, niin olet kastunut. Jos et kuitenkaan kävellyt sateessa, silloin meitä ei kiinnosta kastuitko ja näin väittämä on tosi. Jos kävelet sateessa kastumatta, silloin väittämä on epätosi.
Tämän väittämän osoittaminen todeksi tai epätodeksi tarkoittaa, että täytämme JOS x NIIN y:n sarakkeen. Jos kaikki kohdat ovat totta, silloin propositio on tosi. Muutoin se on epätosi. Voimme täyttää yhden solun sarakkeesta heti ilman katsomatta varsinaista todistusta: sen missä x TAI y on epätosi.

JOS x NIIN y on automaattisesti tosi jos x on epätosi. Muissa tapauksissa meidän pitää täyttää sarake. Tämän tekeminen 100-prosenttisen muodollisesti tarkoittaa, että joudumme aloittamaan kaikkien väittämän termien määritelmistä, tai joudumme siteeraamaan jotain lausetta. Esimerkiksi, jos joku osoittaisi että ”jos kävelet sateessa, niin kastut”, me voimme viitata lauseeseen täyttääksemme kohdat sarakkeista jossa (Henkilö kävelee sateessa) on tosi.

Mutta sanotaan, että meillä ei ole mitään lausetta väitteelle (henkilö hyppää altaaseen). Silloin meidän on mentävä märän määritelmään, joka on “peitetty tai liotettu vedellä”. Me voimme sitten vedota veden ominaisuuksiin, ihmisen ihon ominaisuuksiin ja altaan määritelmään väittääksemme, että jos hyppäät altaaseen, vesi koskettaa kehoasi ja peityt siihen ja sen tähden kastut. Me voimme sitten käyttää tätä määritelmää täyttämään loput kohdat y-sarakkeesta.

Voimme täyttää taulusta loput katsomalla totuustaulua kohdasta JOS x NIIN y, ja päätyä tosiarvoon, joten todistus on valmis.

Totuustaulumenetelmä on kaikkien muiden menetelmien selkäranka, mutta sitä harvoin käytetään tässä muodossa, koska se on aika työläs. Jos mahdollista, sinun kannattaa yrittää nähdä miten muut menetelmät liittyvät tähän.
Muita Boolen algebraan liittyviä asioita
Boolen algebrassa on pari muutakin operaatiota, mutta keskeisimmät ovat EI sekä JA, joiden totuustaulut ovat seuraavat.

Pelkillä TAI, EI sekä JA, on mahdollista rakentaa kaikki muut loogiset operaatiot, myös JOS x NIIN y. Voit rakentaa ne kaikki invertoidulla JA-operaatiolla (NAND), joka yhdistää EI ja JA -operaatiot, tai invertoidulla TAI-operaatiolla, eli NOR, joka yhdistää EI sekä TAI -operaatiot, mutta sähköinsinöörit murehtivat näitä sitten enemmän.
Kvanttorit ja joukko-opin perusteita
Jos mietit joukkoa listana asioita, jossa yhtäkään asiaa ei toisteta, se riittää useimmassa tapauksessa. Matematiikassa on kolme kvanttoria:
- Eksistentiaalikvanttori: Tämä kvanttori sanoo, että joukolla on alkio. Se luetaan “joukossa on olemassa alkio”. Matematiikassa kirjoitamme sen merkillä ∃. Esimerkki kvanttorin käytöstä olisi “on olemassa luonnollinen luku (1, 2, 3,…) joka on jaolla luvulla kolme, joka on sen monikerta” (esim. 6, 9, 12, …).
- Yksikäsitteisyyskvanttori: Tämä kvanttori sanoo, että joukossa on tasan yksi alkio. Matematiikassa se kirjoitetaan ∃!. Se luetaan “on olemassa tasan yksi luonnollinen luku, joka on jaollinen luvulla 3 ja joka on alkuluku” (eli 3).
- Universaalikvanttori: Tämä kvanttori sanoo, että kaikilla joukon alkioilla on tietty ominaisuus. Se luetaan “jokaiselle alkiolle joukossa”. Matematiikassa se kirjoitetaan merkillä ∀. Esimerkki kvanttorista olisi “jokaisella luonnollisella luvulla on olemassa sitä suurempi luonnollinen luku” (luvulle 7 voimme nimetä 8, 9, 10, 100 tai 10¹⁰⁰⁰⁰ esimerkkeinä).
Propositiot matematiikassa
Kuten näit universaalikvanttorin esimerkissä, voimme yhdistää kvanttoreita muodostamaan formaaleja propositioita. Normaalisti määrittelemme näiden propositioiden muuttujat niin, että voimme käyttää niitä myöhemmin. Esimerkiksi, voimme lausua universaalikvanttorin esimerkin “jokaiselle x luonnollisissa luvuissa on olemassa y luonnollisissa luvuissa niin, että y on suurempi kuin x”. Matemaattisesti kirjoittaisimme

Tämän proposition todistamiseksi me kuljemme vasemmalta oikealle. Ensimmäinen termi on ”jokaiselle x”, eli x on syötemuuttuja todistuksessamme. ∈ tarkoittaa, että x tulee kuulua sen jälkeen tulevaan joukkoon, joka on ℕ, luonnolliset luvut. Toinen termi on “on olemassa y”, joten meidän tulee osoittaa, että on olemassa y joka toteuttaa proposition lopun. Viimeisenä meillä on y > x, joka on proposition loppuosa.
Päättelysäännöt
On olemassa monia eri päättelysääntöjä joita voit käyttää, mutta tulet käyttämään niitä jokatapauksessa vaikka et edes niistä tietäisi. Me käytimme disjunktion eliminointia päättelysääntönä todistuksessamme. Haluan kuitenkin näyttää muutaman kvanttoreihin liittyvän päättelysäännön.
- Universaali Instansiaatio: Jos kaikilla joukon alkioilla on jokin ominaisuus, ja x on joukon alkio, silloin x:llä on tuo ominaisuus. Esimerkiksi, kaikki ihmiset ovat kuolevaisia. Sokrates on ihminen. Niinpä Sokrates on kuolevainen. Tätä temppua voi käyttää osoittamalla, että jokin objekti kuuluu johonkin ominaisuuksien joukkoon, kun haluat objektilla olevan jonkin ominaisuuden.
- Eksistentiaalinen Yleistys: Jos objektilla on jokin ominaisuus, silloin on olemassa objekti, jolla on tuo ominaisuus. Esimerkiksi, minulla on tietokone, siispä on olemassa joku jolla on tietokone. Tätä temppua voi käyttää aina kun tietää konkreettisen esimerkin.
- Eksistentiaalinen Instansiaatio: Jos on olemassa jjokin objekti jollain ominaisuudella, silloin voit antaa nimen tuolle elementille ja käyttää sitä todistuksen loppuajan. Esimerkiksi, jos sanon todistavani, että on olemassa jokin luku, joka on jonkin yhtälön ratkaisu, voin antaa sille nimen ja käyttää sitä lopun todistuksen ajan sanomalla “olkoon k tämän yhtälön ratkaisu”.
Nämä ovat teknisiä juttuja, joita en aktiivisesti ajattele edes käyttäväni, mutta on avuksi tietää että ne ovat olemassa.
Tunne keskeiset todistusmenetelmät
Nyt voimme alkaa käsitellä todistuksia. Tässä osiossa käsittelemme keskeisiä todistustyyppejä ja annamme joitain ehdotuksia milloin käyttää niitä. Ohjelmoijat voivat pitää näitä menetelmiä eräänlaisena viitekehyksenä. Ne antavat jonkinlaista rakennetta, ja sitten voit itse täyttää loput yksityiskohdat.
Suora todistus
Palatkaamme takaisin todistukseen, jonka teimme totuustauluilla. Me emme koskaan täyttäneet ensimmäistä riviä (henkilö kastuu) koska meitä ei kiinnostanut se tapaus jossa henkilö ei kävellyt sateessa tai ei hypännyt altaaseen. Toisin sanoen, me tarkastelimme ainoastaan tapauksia, joissa x on tosi todistuksessamme. Sellainen todistus tunnetaan nimellä suora todistus. Yleiset askeleet suoraassa todistuksessa ovat
- Oleta, että x on tosi.
- Käytä sitä seikkaa, että x on tosi, näyttämään, että myös y:n on oltava tosi.
Me oletimme, että henkilö käveli sateessa tai hyppäsi altaaseen, ja sitten näytimme, että vesi oli koskettanut henkilön ihoa ja se kasteli hänet (minun olisi pitänyt valita esimerkki, missä ei käytetä ilmaisuja “henkilön iho” ja “kastua”.). Koska me tarkastelimme kaikkia tapauksia erikseen, todistus tunnetaan nimellä kaikkien tapausten läpikäynti.
Todistus: Ei ole olemassa suurinta mahdollista luonnollista lukua
Propositiona on “kaikille luonnollisille luvuille on olemassa suurempi luonnollinen luku”. Helpoin tapa todistaa tämä propositio on keksiä joukko askelia, jossa otetaan luonnollinen luku ja sitten tuotetaan suurempi luonnollinen luku. Voimme tehdä sellaisen joko lisäämällä luvun yksi tai kertomalla luvulla kaksi (en laske nollaa luonnolliseksi luvuksi.).

Tämänkaltainen todistus tunnetaan nimellä rakenteinen todistus, sillä me olemme keksineet keinon rakentaa esimerkin, jolla propositio pätee jokaisella luonnollisella luvulla.
Ääretön totuustaulukko?
Huomaat, että totuustaulu yllä esitetylle todistukselle olisi joutunut olemaan ääretön. Me tarvitsemme yhden rivin jokaista mahdollista luonnollista lukua varten, mikä on ongelma koska emme voi tarkastaa onko jokainen rivi totta. Onneksi voimme päästä pois tästä ongelmasta, koska meidän tarvitsee tarkistaa vain, että se pätee jokaiselle käyttämällemme luonnolliselle luvulle. Tavallaan todistuksemme on enemmänkin pohja jolla osoittaa proposition olevan totta aina sille tietylle tapaukselle, jonka parissa työskentelemme.
Tunnetumpi esimerkki on differentiaalilaskennan/reaalianalyysin raja-arvot, jotka perustuvat siihen miten lähelle haluat päästä vastausta. Esimerkiksi, jos meillä on vaikka raja-arvo

Muodollisesti meillä on
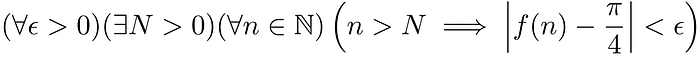
Yksinkertaisimmin ilmaistuna, tämä kaava sanoo, että me voimme päästä niin lähelle kuin haluamme arvoa π/4 (ϵ on se luku miten lähelle haluamme päästä vastausta) summaamalla äärellisen määrän termejä (N on termien minimilukumäärä). Sanokaamme, että haluamme laskea ensimmäiset 100 desimaalia luvusta π/4. Siinä tapauksessa, meitä kiinnostaa ainoastaan ϵ = 1/10¹⁰⁰ ja niinpä totuustaulussamme olisi vain yksi rivi. Me voimme sitten sijoittaa tuon arvon ϵ määrittääksemme raja-arvon avulla N ≈ 69.
Todistus: Pythagoraan lause
Pythagoraan lauseella on tässä vaiheessa yli 100 todistusta, mutta näytän suosikkini. Tämän todistuksen ymmärtämiseksi ainoa mitä pitää tietää on
- kolmion kulmien summa on 180 astetta,
- suorien kulmien suuruus on 90 astetta,
- nelikulmion pinta-ala lasketaan kanta kertaa korkeus,
- ja kolmion pinta-ala on kanta kertaa korkeus jaettuna kahdella.
Huomaa, että kun on tiedossa neliöiden sivut ja suora kulma, pinta-alan laskeminen on varsin luonnollista.

Ainoa mitä tehdään on järjestellään kolmiot muodostamaan neliö (jonka voit tehdä ensimmäisen ja viimeisen faktan perusteella), sitten lasketaan pinkin neliön pinta-ala kahdella tavalla:
- Koska se on neliö, voit laskea sen pinta-alan neliöimällä sivun pituus: c².
- Vaihtoehtoisesti voit laskea suuren neliön pinta-alan (Suuri neliö: (a + b)² = a² + 2ab + b²) ja sitten vähentää kolmioiden pinta-alat (Yksi kolmio: ab/2, neljä kolmiota: 4 (ab/2) = 2ab). Jos teet niin, tulee tulokseksi a² + 2ab + b² – 2ab = a² + b².
Koska molemmat kaavat kuvaavat samaa pinta-alaa, niiden on oltava yhtäsuuret, mikä tarkoittaa a² + b² = c², ja Pythagoraan lause on todistettu.
Kontrapositiiviset todistukset
Koska meillä on suoria todistuksia, voitaisiin myös spekuloida, että on olemassa epäsuoria todistuksia. Se pitää paikkansa. Epäsuoran todistuksen ymmärtämiseksi tarkastellaan totuustaulua JOS x NIIN y.

Ainoa tapa, jolla propositio olisi epätosi, on jos x on tosi, mutta y epätosi. Proposition osoittaminen todeksi on mahdollista osoittamalla, että me emme koskaan saavuta tapausta, jolloin x on tosi mutta y epätosi olettamalla, että y on epätosi ja näyttämällä että x ei voi olla tosi. Tämän kaltainen epäsuora todistus tunnetaan nimellä kontrapositiivinen todistus. Latinaksi sen nimi on modus tollens.
Todistus: Neliöt ja parilliset luvut
Esimerkiksi, tarkastellaan väittämää “jos n² on pariton, silloin n on parillinen”. Suora todistus toimisi tässä, kun vetoamme aritmetiikan peruslauseeseen, mutta pidän kontrapositiota yksinkertaisempana. Tässä tapauksessa haluamme näyttää, että “jos n on pariton, silloin n² on pariton”. Koska meillä ei ole parempaakaan tekemistä, tarkastellaan määritelmiä. Jos me tarkastelemme parittoman luvun määritelmää, huomaamme että luonnollinen luku x on pariton jos ja vain jos on olemassa luonnollinen luku k siten että 2 k – 1 = x. Koska n on pariton oletuksemme perusteella, asetamme m sellaiseksi luvuksi, että 2 m – 1 = n Eksistentiaalisen Instansiaation avulla. Sitten voimme sijoittaa 2 m – 1 lausekkeeseen n² ja algebran avulla saada 4 m² – 4 m+ 1. Tämä voidaan ottaa tekijöiksi 2 ( 2 m² – 2 m ) + 1 tai 2 ( 2 m² – 2 m + 1) – 1. Tästä lausekkeesta voimme todeta, että n² on pariton, koska me voimme asettaa k siten, että 2 k – 1 = n², eli siis k = 2 m² – 2 m + 1.
Kontrapositiivisen todistuksen ensimmäisen askeleen jälkeen loput todistuksesta voi olla mitä tahansa. Todistus yllä on suora todistus sille, että “jos n on pariton, niin n² on pariton”.
Todistus vastaväittämällä
Todistus vastaväittämällä on toisenlainen epäsuora todistus. Se eroaa muunlaisista todistuksista, sillä se nojaa rajoitukseen, että loogisten järjestelmien tulee olla myös johdonmukaisia ollakseen hyödyllisiä. Yleinen vastaväittämällä todistamisen menetelmä on näyttää, että jos väittämä olisi epätosi, siitä seuraa ristiriita.
Todistus vastaväittämällä toimii hyvin kaiken kanssa, mutta haluan keskittyä epärakenteisten todistusten esimerkkiin. Toisin kuten rakenteiset todistukset, epärakenteiset todistukset eivät mahdollista tapaa rakentaa esimerkkejä. Sen sijaan ne käyttävät useita olemassaololauseita kuten kyyhkyslakkaperiaate tai väliarvolause.

Todistus: Irrationaaliluvuissa toistuu ainakin yksi numero äärettömän monta kertaa
Tarkastellaan väittämää “irrationaaliluvun desimaaliesityksessä toistuu ainakin yksi numero äärettömän monta kertaa”. Oletetaan, että mikään numero ei toistu äärettömän monta kertaa irrationaaliluvun desimaaliesityksessä. Siinä tapauksessa kaikkien numeroiden tulee esiintyä äärellisen monta kertaa. Koska meillä on vain kymmenen numeroa, joista jokainen esiintyy äärellisen monta kertaa, numeroiden yhteenlaskettu lukumäärä tulee olla äärellinen. Me kuitenkin tiedämme, että irrationaaliluvuilla on oltava ääretön määrä numeroita. Meillä on ristiriita. Oletuksemme on oltava epätosi, mikä tarkoittaa että väittämämme on tosi, ja todistus on valmis. Koska me emme maininneet mikä tuo numero on, tämä todistus ei voi olla rakenteinen.
Kyyhkyslakkaperiaate
Minun onnistui keksiä todistus käyttämällä kyyhkyslakkaperiaatetta. Jotta sinäkin voisit kokea saman, tässä on seitsemän todistusta, joissa kyyhkyslakkaa on käytetty.
Matemaattinen induktio
Matemaattinen induktio on eräänlainen suora todistus. Siinä näytetään, että propositio on tosi jollekin perustapaukselle, sitten näytetään että perustapaus yhdistettynä propositioon (induktiohypoteesi) tarkoittaa, että propositio pätee kaikissa tapauksissa. Useimpien todistusten kanssa perustapaus on jokin luonnollinen luku k, ja “kaikki tapaukset” viittaavat kaikkiin luonnollisiin lukuihin, jotka ovat suurempia tai yhtä suuria kuin k.
Induktiota usein verrataan dominoihin, induktioaskel on kuin jokaisen dominopalikan pystytys ja perustapaus on ensimmäisen dominon kaataminen.
Todistus: Ensimmäisen N parittoman luvun summa
Induktio toimii hyvin pulmiin, joihin liittyy summaamista, seuraavakaan ei ole mikään poikkeus. Me voimme esittää ensimmäisen N parittoman luvun summan
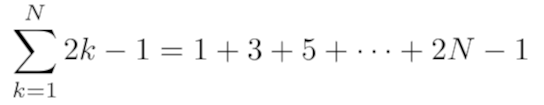
Niille jotka tuntevat ohjelmointia, tämä muoto voidaan esittää for -silmukoina.
Jos et jo tunne kaavaa, kannattaa ensin tarkastella muutamaa ensimmäistä termiä.

Nämä näyttävät ensimmäisiltä lukujen neliöiltä. Esitämme konjektuurin (matematiikan kielellä “arvaus”) että ensimmäisten N parittoman luvun summa on N². Nyt todistamme sen. Me olemme jo osoittaneet perustapauksen pätevän, sillä 1 = 1². Seuraavaksi tarkastelemme induktioaskelta. Oletamme, että olemme osoittaneet ensimmäiset N tai N – 1 lukua. Tässä tapauksessa sanon N – 1 (kumpikin toimii, joten voit heittää vaikka kolikkoa jos et osaa valita), joka tarkoittaa

Me joudumme käyttämään tätä tulosta soveltaaksemme sitä luvun N – 1 jälkeen tulevaan lukuun, joka on N. Jos olisimme valinneet N, silloin käsittelisimme tapausta N + 1. Juuri nyt meillä on kaksi tapaa laskea summa:
- Sijoita N kaavaan ja laske N².
- Lisää seuraava termi (2 N +1) summaan.
Molemmissa tapauksissa pitäisi saada N². Tässä kohtaa algebran avulla käytämme induktiohypoteesia.

Tämä todistus käytti heikon induktion menetelmää, koska me oletimme proposition pätevän vain lukuun N – 1 asti. Vahvassa induktiossa oletetaan, että propositio pätee kaikille arvoille alle N. Vahva induktio on yhtä hyvä kuin heikko induktio, vahvalla induktiolla on vain vahvempi induktio-oletus.
Todistus: Aritmetiikan peruslause (vahva induktio)
Aritmetiikan peruslause sanoo, että jokainen ykköstä suurempi luonnollinen luku on hajoitettavissa alkulukutekijöihin. Esimerkiksi luku 12 voidaan kirjoittaa 2² × 3, kun taas 17 voidaan kirjoittaa 17. Tässä on todistus sille, että voit hajoittaa jokaisen luvun alkulukutekijöihinsä.
Yksikäsitteisyyden todistaminen vaatii tietoa jakosäännöistä, joita en ole käsitellyt.
Joukkoonkuuluvuusperiaate
Joillekin propositioille induktiotodistus on liian hankalaa, mutta se saattaa silti toimia. Vaihtoehtona voimme käyttää joukkoonkuuluvuusperiaatetta. Sen mukaan jokaisella luonnollisten lukujen osajoukolla on ainakin yksi alkio. Kun käytämme joukkoonkuuluvusperiaatetta todistuksessa vastaväittämän avulla, aloitamme olettamalla, että on olemassa luonnollisten lukujen ei-tyhjä joukko, jolle todistettava propositio ei päde. Kutsumme tätä epätodeksi joukoksi. Sitten sovellamme joukkoonkuuluvuusperiaatetta valitsemaan kyseisen joukon pienimmän alkion. Sitten käytämme tuota alkiota osoittamaan ristiriidan. Yleensä osoitetaan jompi kumpi:
- että väittämä on tosi epätoden joukon pienimmälle alkiolle, tai
- että epätoden joukon pienin alkio ei ole joukon pienin alkio.
Kummassakin tapauksessa ainoa tapa välttää ristiriitaa on, että epätosi joukko on tyhjä.
Todistus: Aritmetiikan peruslause
Vaikka olemmekin jo todistaneet tämän, on hyvä esittää vaihtoehtoinen todistus. Tässä todistuksessa näytämme, että propositio pätee epätoden joukon pienimmälle alkiolle.
Tämän todistuksen ensimmäinen osa tulisi näyttää varsin samanlaiselta kuin vahvalla induktiolla todistaminen.
Todistus: kahden neliöjuuren irrationaalisuus
Tässä tapauksessa käytämme tietyn tyyppistä todistusta, joka perustuu joukkoonkuuluvuusperiaatteeseen, nimeltään äärettömän laskeutumisen menetelmä. Äärettömän laskeutumisen menetelmässä oletetaan, että ollaan löydetty joukon pienin alkio tietylle luonnollisten lukujen joukolle, ja sitten käytetään tuota alkiota tuottamaan pienempi luonnollinen luku. Sitä kutsutaan äärettömäksi laskeutumiseksi, koska todistusta voi käyttää uudelleen äärettömän monta kertaa tuottamaan vieläkin pienempiä lukuja.
Aivan kuten aiemminkin, olisimme voineet kirjoittaa tämän todistuksen induktiolla, jossa jokainen askel antaa seuraavan osoittajan ja nimittäjän.
Milloin käyttää mitäkin todistusmenetelmää
Jos voisin antaa absoluuttisen vastauksen siihen milloin kutakin todistusmenetelmää voisi käyttää, olisin jo voittanut Fieldsin mitalin. Voin kuitenkin joitain vinkkejä antaa:
- Todistus ristiriidalla: tämä on aina mahdollisuus.
- Todistus vastaväittämällä: Jos todistettavan asian seurauksen kanssa on helpompaa työskennellä kuin sitä edeltävien oletusten, silloin kannattaa kokeilla vastaväittämää.
- Suora todistus: Suorat todistukset ovat hyviä propositioiden kanssa, jotka ovat muotoa “on olemassa x kuuluu A:han siten, että P”, jossa P on jotain mitä voi manipuloida algebralla tai muilla työkaluilla.
- Epäsuorat todistukset: Epäsuorat todistukset ovat hyviä propositioihin, jotka ovat muotoa “on olemassa x kuuluu A:han siten, että P”, jossa P nojaa johonkin olemassaololauseeseen, kuten kyyhkyslakkaperiaate, väliarvolause tms.
- Induktiotodistus: Induktio on hyvä aina kun voi löytää pienemmän version pulmasta todistettavan pulman sisällä. Esimerrkiksi, ensimmäisten n luvun neliön summa voidaan kirjoittaa ensimmäisten n – 1 neliön summana plus n:s neliö, joten induktio toimii.
- Todistus joukkoonkuuluvuusperiaatteella: Joukkoonkuuluvuusperiaate toimii aina kun työskentelee kokonaislukujen tai rationaalilukujen parissa, ja haluaa osoittaa ristiriidan.
- Kaikkien tapausten läpikäynti: Suosittelen kaikkien tapausten läpikäyntiä vain, kun tapausten lukumäärä on pieni, tai viimeisenä oljenkortena.
Muuta pulmaa
Nyt kun olemme listanneet yleisimmät todistusmenetelmät, puhutaan hieman muutamista tempuista. Jos jää jumiin johonkin tiettyyn pulmaan, voit koittaa
- esittää heikomman väittämän (esim. jos pitää osoittaa, että kaikkien ei-täydellisten lukujen neliöjuuret ovat irrationaalisia, voit osoittaa, että kaikkien alkulukujen neliöjuuret ovat irrationaalisia),
- esittää yleisemmän väittämän (esim. triomino-peli, jossa osoitetaan että voi laittaa tyhjän neliön mihin tahansa yhden ainoan paikan sijaan),
- tai osoittaa jonkin asiaan liittyvän tai vastakkaisen väittämän (esim. jos halusit osoittaa, että “jos n² on parillinen, silloin n on parillinen”, voit koittaa osoittaa “jos n on parillinen, silloin n² on parillinen” saadaksesi idean siitä mitä sinun tulee tehdä).
Usein ongelman muuttaminen antaa idean siitä minne pitää mennä seuraavaksi. Heikomman väittämän todistuksessa löytää usein todistuksen, joka hajoaa kun alkuperäistä väitettä soveltaa. Siinä kohtaa voi joko yrittää paikata todistusta ja käsitellä erikoistapausta tai keksiä uuden todistuksen, joka täysin välttää hajoamisen. Toisaalta, vahvemman väittämän todistaminen usein siivoaa pois irrelevanttia informaatiota, joka liittyy heikompaan väittämään. Viimeisenä asiaan liittyvän käänteisen väittämän todistaminen voi auttaa ymmärtämään sitä mitä pitää todistaa.
Etsi invariantteja ominaisuuksia
Joskus joutuu käsittelemään pulmia, jotka saattavat vaatia suuremman, mahdollisesti äärettömän, avaruuden tutkimista. Monen tällaisen ongelman tapauksessa voi etsiä ominaisuutta, joka sopii kaikkialle. Me nimitämme sellaista ominaisuutta invariantiksi. Useimmissa tapauksissa nämä invariantit voidaan kirjoittaa jonkinlaisen funktion muotoon, jossa tietyt koordinaatit ovat vakioita. Esimerkiksi, eräs tällainen invariantti on Eulerin karakteristika χ:

Voit soveltaa tätä invarianttia ja vastaavia osoittamaan, että et voi ratkaista ongelmaa pallopinnalla tai tasopinnalla, mutta voit kylläkin toruspinnalla.
Eräs nimekkäimmistä esimerkeistä tulee vuoden 2011 matematiikkaolympalaisista:
563 opiskelijasta ainoastaan 20 sai tämän kysymyksen oikein. Jos kykenet löytämään jonkin invariantin, tämä ongelma muuttuu triviaaliksi. Voit laittaa videon paussille sen jälkeen kun näet kolmioita ja yrittää katsoa osaatko ratkaista ongelman.
Todistus: Conwayn sotilaat
Tämän koko pulman ja sen ratkaisun selittämiseen tarvitaan kokonainen toinen artikkeli. Sen sijaan linkkaan kaksi videota: yksi selittää pelin ja toinen sen todistuksen.
Yllä on pelin selitys.
Alla on todistus.
Liitän mukaan todistuksen esimerkkinä, koska se on varsin helppo seurata, haluan jakaa lisäresursseja todistuksista, haluan antaa tiettyjä esimerkkejä siitä miten antaa numeroita pulmille, joilla ei vaikuta olevan numeroita, joiden perusteella tuottaa invariantteja.
Todistus: Punaiset, valkoiset ja vihreät pallot
Olkoon sinulla 2000 vihreää palloa. Voit tehdä palloilla seuraavaa:
- Vaihtaa kaksi punaista palloa yhteen vihreään palloon tai päinvastoin.
- Vaihtaa kaksi valkoista palloa vihreään palloon tai päinvastoin.
- Vaihtaa kaksi vihreää palloa punaiseen palloon ja valkoiseen palloon tai päinvastoin.
Nyt esitän kaksi kysymystä:
- Onko mahdollista olla 1003 punaista palloa äärellisen määrän yllä esitettyjä vaihtoja jälkeen?
- Mikä on minimimäärä palloja, joita voi olla?
En anna vastausta tähän, mutta annan yhden vihjeen: yritä antaa palloille numeroita niin, että vaihdot ovat järkeviä. Siitä eteenpäin voit yrittää etsiä invarianttia, joka auttaa vastaamaan kysymykseen. Minua kiinnostaa nähdä miten ihmiset yrittävät ratkaista tämän ongelman.
Vaikka yllä esitetyt menetelmät tulevatkin esiin matematiikan kaikilla osa-alueilla, jotkut alueet käyttävät joitain todistuksia enemmän kuin toiset. Reaalianalyysissa käytetään paljon aikaa tiettyjen ominaisuuksien raja-arvojen etsimiseen, joten käytetään usein temppuja kuten nollan summaaminen kolmioepäyhtälöön tai kaikki tässä Terrence Taon artikkelissa esitetyt temput. Modernissa algebrassa halutaan usein osoittaa, että jokin struktuuri liittyy siihen struktuuriin minkä kanssa halutaan työskennellä. Graafiteoriassa halutaan tarkastella aligraafeja. Paljon pidempi lista löytyy sivulta tricki.org, vaikka sivu vaikuttaakin epäaktiiviselta.
Satunnaisia vinkkejä
Tässä osiossa on joitain vinkkejä, joille ei kannata välttämättä kirjoittaa kokonaista omaa osiotaan:
- Jos et tiedä mistä aloittaa, kirjoita ylös kaikki määritelmät tai lauseet, jotka mielestäsi ovat relevantteja.
- Mitä enemmän vaivaa näet alussa, sitä enemmän voit antaa matematiikan mennä omaa reittiään.
- Työskentele vain parin yksittäistapauksen parissa. Esimerkiksi, yritä työskennellä nollan tai ykkösen kanssa, tai minkä tahansa joka saattaisi olla erikoistapaus.
- Jos et osaa keksiä mahdollisia erikoistapauksia, käy läpi useampi tapaus ja katso löydätkö jonkun kaavan.
- Usean muuttujan ongelmissa määrittele yksi muuttuja toisten muuttujien avulla. Esimerkiksi jos pulmassa on A ja B, kokeile määritellä B = A + k tai B = c A.
- Lisää nolla tai kerro ykkösellä ja kirjoita lauseke eri muotoon niin, että sen kanssa on helpompaa työskennellä.
- En piirrä kuvaajia ellen ole geometrian parissa, mutta monet ihmiset suosivat piirtää kuvaajia ymmärtääkseen mistä on kyse.
Tämä artikkeli on jo tarpeeksi pitkä, mutta on paljon enemmänkin eri temppuja kuin mitä listasin.
Lisälukemista
Tämä artikkeli ei todellakaan ole ainoa resurssi matemaattisista todistuksista, joten haluaisin mainita muitakin:
- 3blue1brownin kanava on hyvä, mutta suosittelisin Lockdown Math -sarjan viimeisintä videota.
- Daniel J. Vellemanin How to Prove It: A Structured Approach vaikuttaa olevan standardikirja todistuksille. Melkein kaikki aihepiirit mainitaan ja niitä käsitellään kirjassa, ja siinä on paljon harjoituksia.
- Tässä on pruju joka käsittelee sitä jos sattuu jäämään jumiin todistuksissa.
- Minun juttusarjani raja-arvoista näyttää muutaman erilaisen todistuksen, mutta käsittelee myös reaalianalyysia.
- Tämän videon ja tämän videon kanavat käsittelevät omilla videoillaan todistuksia.
- Michael Pennilla on yli tuhat videota eri aiheista.
- Terrence Taolla on kirja matikkakilpailutehtävistä varttuneemmille tieteenharjoittajille.
Viimeisenä, artikkelissani Beyond Calculus: The Math Classes You Didn’t Take on paljon resursseja.