Tarkat kuvaukset vaikutuksista eivät ole hiustenhalkomista; se on paljon kaivattua tarkkuutta, jolla vältetään sekaantuminen äärimmäisen monimutkaiseen ja tiheään tieteelliseen ja yhteiskunnalliseen debattiin, jota käydään COVID-19 rokotteiden ympärillä. Se ei tarkoita, että 95% ihmisistä ovat saaneet suojan sairaudelta rokotteella — mikä on yleinen väärinkäsitys rokotesuojasta, joka löytyy myös Lancet Infectious Diseasesin pääkirjoituksesta.

Tämä julkaistiin kirjeenvaihdossa maaliskuun 8. päivänä julkaistussa The Lancetin numerossa, joka on johtava vertaisarvioitu lääketieteen tiedejulkaisu. Se painottaa, että jopa aiheeseen keskittyneissä tiedepiireissä väärinymmärrykset raportoitujen rokotetehokkuuslukujen tarkoituksesta ja merkityksestä ovat edelleen läsnä. Jos tiedeyhteisö tekee virheen omissa tulkinnoissaan, se voi vaikuttaa poliittisten päättäjien toimintaan, jopa kaikkein koulutetuimpiin, ja tämä väärinymmärrys taas vuorostaan voi välittyä kansalle.

Viime viikkoina olen nähnyt todisteita artikkeleista, joilla korjataan joitain varhaisimpia väärinkäsityksiä, joista The Lancetin kirjeenvaihto oli huolissaan. Kuitenkin vielä kaameampi väärinymmärtämisen ja misinformaation muoto on jäljellä, ja sitä on kaikkialla.

It's actually pretty simple math. If you get Covid and you've been vaccinated, you're about 100 times less likely to die.

— Dr. Tom Frieden (@DrTomFrieden) July 27, 2021

Tom ei ole kuka tahansa lääkäri. Hän on entinen Center for Disease Controlin johtaja presidentti Barack Obaman hallinnossa. Hän myös levittää vaarallista misinformaatiota COVID-19 rokotteista. Se tulee aiheuttamaan väärinymmärrystä oikeassa elämässä, mikä voi johtaa monen ihmisen kuolemaan ja pahentaa pandemiaa.

Tri. Tom on väärässä. About niin väärässä kuin vain voi olla. Reaalimaailman data on näyttänyt, että rokotettujen kuolleisuus, jos he saavat COVIDin, voi olla 3-5.7 kertaa suurempi [1] kuin rokottamattomien.

Hyväksyttävä katastrofaalinen virhe

Entinen CDC:n johtaja tekee jotain mitä minä kutsun hyväksyttäväksi katastrofaaliseksi virheeksi. Tämänkaltainen virhe on sellainen joka sallitaan tehdä kun tekijä kuvittelee olevansa asiassa oikeassa. Argumentit ja tilastot, joita käytetään jokaisen ihmisen rokotetuksi saamiseen COVIDin varalta saavat paljon vähemmän syynäystä ja hyväksytään todeksi paljon helpommin kuin argumentit tai tilastot, jotka voisivat olla tuota tavoitetta vastaan.

Kun CDC:n entinen johtaja, tai kuka tahansa muu, sanoo että COVIDin saanut on 100-kertaisesti todennäköisemmin kuolemassa jos hän ei ole saanut rokotetta rokotettuun verrattuna, ei ole väliä sillä miten paisuteltu tuo luku on. Tämä annetaan hänelle anteeksi huolimatta siitä miten epätarkka luku on. Tavoite on saada kaikki rokotetuksi, eikä niinkään totuuden puhuminen, vaikuttaa olevan se mikä merkkaa.

Hyväksyttäviä katastrofaalisia virheitä on paljon.

Rokotteiden tehokkuus

Ymmärtääksemme miksi ihmiset väittävät, että nämä ihanat lisähyödyt ovat olemassa, me joudumme valitettavasti soveltamaan matematiikkaa. Mutta niin tekemällä vältämme sekaannuksen, ja vaarallisen disinformaation viranomaisilta ja niiltä, jotka haluavat vakuutella kaikille että ottakaa rokote.

Ymmärtääksemme rokotteiden tehokkuutta, Pfizer–BioNTechin mRNA BNT162b2:n kliinisessä kokeessa ollut diagrammi on erittäin hyödyllinen.

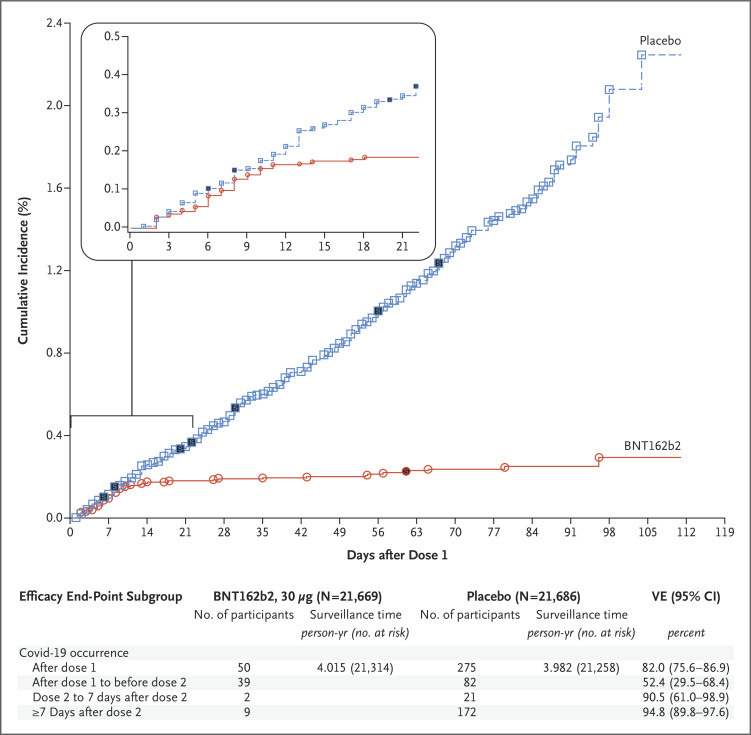
Punainen ympyräviiva näyttää, että rokotteen saaneilla, joita oli 21 669 ihmistä, infektion tarttuvuus laski. Keskimääräinen päivien lukumäärä yksittäisten infektioiden välillä kasvoi. Tuloksena on, että tietyn ajanjakson yli niiden ihmisten yhteismäärä, jotka saivat infektion, oli kuin olikin todella paljon matalampi kuin rokottamattomien infektioiden määrä.

Tässä kohtaa aiempi lausunto The Lancetissa “niistä jotka sairastuisivat COVID-19:n mikäli he eivät olisi ottaneet rokotetta” astuu mukaan kuvioihin. On järkevää olettaa, että punainen viiva muistuttaisi sinistä viivaa mikäli ryhmä ei olisi saanut rokotetta. Täten voisi laskea neliöiden lukumäärän sinisellä viivalla, joita esiintyy punaisten pallojen välissä, ja saada suhdeluvun siitä miten monta rokottamatonta saisi tartunnan per yksi rokotettu henkilö tietyssä ajassa.

Tehokkuussuhdeluku (taulukossa VE) on tapa yrittää tehdä tämä. Tähän tulee kuitenkin mukaan yksi kompleksisuuden lisätaso. Tutkijat kohtelevat tutkimuksessa olevia koehenkilöitä niinkuin heillä ei olisi toisiinsa nähden eroa. Joka päivä kun tutkimukseen otetaan mukaan henkilö, observaabelina pidetään henkilöpäivää. Jokainen tiettynä päivänä tarkkailtava henkilö mitataan ja lisätään henkilöpäivien mittariin. Tutkimuksen lopulla havaittujen infektioiden määrä jaetaan lasketulla henkilöpäivien lukumäärällä ryhmässä.

Esimerkiksi, jos kahta ihmistä havainnoidaan neljän päivän ajan, se on yhteensä kahdeksan henkilöpäivää. Jokaisen henkilön on mahdollista saada infektio kunakin päivänä, elleivät he ole jo infektoituneita. Se tekee yhteensä kahdeksan eri mahdollista hetkeä saada infektio. Kuitenkin, kun infektio on saatu, joku ei voi enää saada infektiota, jolloin henkilöä ei enää lasketa henkilöpäiviin. Tässä tietyssä tutkimuksessa käytettiin eri mittaria kuin yksi päivä, mutta idea pysyy samana.

Päivän lopulla tehokkuuslaskelma on tulosta siitä, että on laskettu asioita ja jaettu kokonaismäärä toisella luvulla. Me voimme ottaa lasketut luvut ja jakaa ne itse tullaksemme samoihin tehokkuuslukuihin. Käyttäkäämme dataa ≥ 7 päivää 2. annoksen jälkeen. Meillä on 21,314 ihmistä ja 4.015 aikayksikköä rokotettujen ryhmässä, ja 21,258 ihmistä ja 3.982 aikayksikköä rokottamattomien ryhmässä. Nyt me vertaamme tarttuvuutta, mikä oli 9 ja 172 havaittua infektiota näissä ryhmässä vastaavasti.

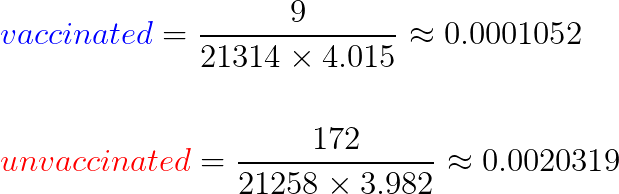
Lopuksi me otamme kaksi suhdelukua ja vertaamme niitä ja laskemme luvun, joka edustaa prosenttilukua nimeltä tehokkuus.

Tässä on tehokkuus taulukosta. Miinustamalla 1:stä mahdollistaa meidän esittää luku niin että suurempi on parempi, sen sijaan että käytettäisiin “golf-sääntöjä” missä pienempi on parempi. Lasku itsessään ei ole harhaanjohtava kun tietää miten se on johdettu. Mutta on tärkeää pitää mielessä idea mistä me puhumme kun me puhumme infektioista tietyssä aikayksikössä. On täysin järkevää vertailla infektioastetta kahden ryhmän välillä tällä tavoin.

Tämä ero on vieläkin tärkeämpi silloin, vaikka me emme tiedä näiden rokotteiden aikaansaamaa riskivähenntystä koeolosuhteissa, kun me emme tiedä voisiko se vaihdella ja miten jos rokotteet olisi annettu populaatioihin eri altistusaikoina, eri tartuntatasoilla ja hyökkäysasteilla. [2]

Reaalipopulaatiot

Israel tarjosi vilauksen Pfizer–BioNTech mRNA BNT162b2 -rokotteen todellisen maailman dynamiikkaan. Suuressa tutkimuksessa, joka on julkaistu toukokuussa 2021 The Lancetissa, käytiin läpi kansallista dataa, jota oli kerätty valtion rokotusohjelmasta. Kerätty data kykeni identifioimaan rokotteen saaneet kunakin päivänä, sen milloin heillä oli diagnosoitu COVID, oliko heillä oireita vaiko ei, ja sen milloin he menivät sairaalaan, joutuivatko he tehohoitoon ja kuolivatko he. Tutkimus on varsin läpikotainen, vaikka se kylläkin sisälsi virheitä, joista osaa ei ole täysin korjattu. Mutta voimme hypätä suoraan tutkimaan tehokkuuslukuja ja korjaamaan virheitä. Käytämme sivun 1825 taulukossa 4 esitettyjä lukuja.

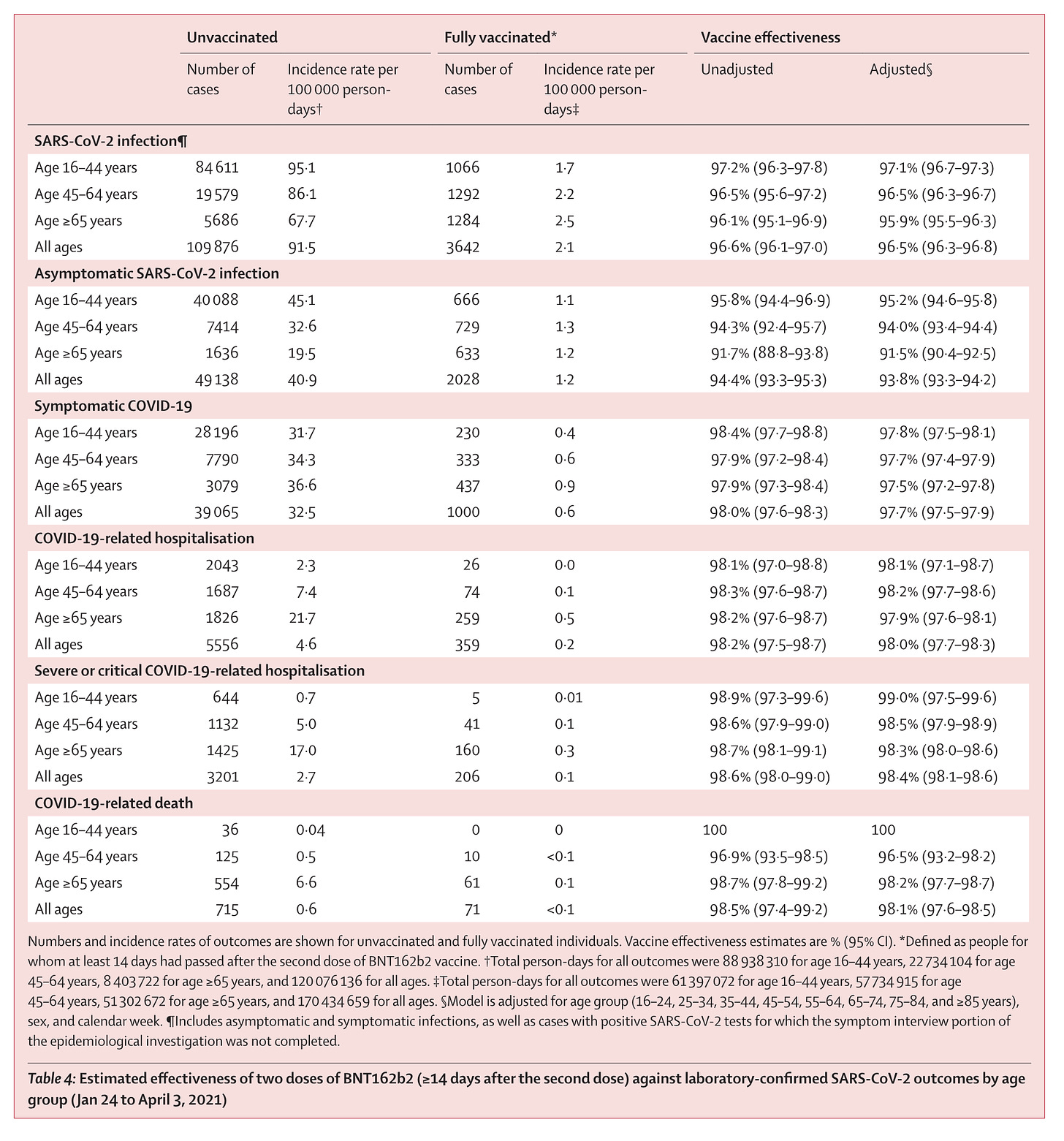
Yläreunan valkoinen laatikoo sisältää infektioiden lukumäärät, joita tutkimuksen aikana oli havaittu. Voimme käyttää kaikkia ikäryhmiä (All Ages). Rokottamattomien ja rokotettujen infektiot kaikille ikäryhmille olivat 109,876 ja 3,642 vastaavasti. Aivan kuten aiemmin, me tarvitsemme henkilöpäiviä (havaittu kokonaisaika) molemmille. Nämä esitetään alemmassa taulukossa rokotttamattomille ja rokotetuille, ja ne ovat 120,076,136 ja 170,434,659 vastaavasti.

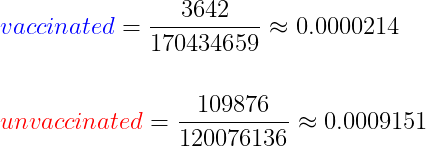
Tarkasteltaessa laskettuja suhdelukuja, nähdään että 91.5 taulukon punaisessa neliössä vastaa meidän laskemaamme rokottamattomien suhdelukua, ja samalla tavoin 2.1 sinisessä laatikossa vastaa laskemaamme rokotettujen suhdelukua. Meidän pitäisi kertoa molemmat luvut 100,000:lla, sillä ne ovat esiintyvyyslukuja 100,000 henkilöpäivää kohden, jotta ne olisivat samoja kuin taulukossa.

Seuraava askel on identtinen Pfizerin kolmosvaiheen kokeen kanssa. “Rokotteen tehokkuusestimaatit laskettiin (1 – IRR) × 100” (esiintyvyysaste, Incidence Rate Ratio, IRR)

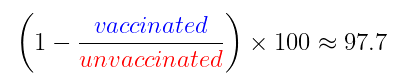
Lukemamme näyttää olevan 1.1% suurempi kuin taulukossa. Selityksiä tälle on kaksi. Yksi on, että heidän korjatessaan joitain lukuja, he eivät päivittäneet tehokkuuslukua. Toinen selitys on, että kirjoittajat ajoivat laskelmat raakadatalla, mitä meillä ei ole, eräiden tilastollisten ohjelmien [3] lävitse estimoidakseen rajat (sulkeissa esiintyvät luvut, joista käy ilmi liikkumisväli estimaateille), jotka antavat heille vivahteikkaamman estimaatin esiintyvyysluvulle kuin heidän lukijalle esittämänsä luvut — meidän laskelmalle ovat sovussa taulukon lukujen kanssa.

Tämä ei ole liian tärkeää, sillä nämä ovat yksinkertaisesti arvioita, joita tutkijat tekevät havaintojen perusteella. Nämä estimaatit muuttuvat ajan mittaan eri populaatioissa. Sellaisia on hyvä olla, mutta niiitä ei tulisi pitää eksakteina.

Ne eivät ole myöskään suurimpien ongelmien lähde. Voidaan katsoa raakalukuja ilman, että lasketaan tehokkuuslukemia ja päätellä siitä, että kyllä, infektioasteet olivat huomattavasti pienemmät. Heidän laskelmissaan olevat erot tehokkuusluvuissa voidaan jättää huomiotta.

Seuraavaksi kuitenkin siirrymme siihen mikä on misinformaation lähde. Se ei ole raportin itsensä vika, vaan seurausta siitä, että liian moni ihminen esittää tietävänsä mistä hän puhuu ja että hänellä olisi auktoriteettia tulkita lukuja joita hän ei ymmärrä.

Rokotteen tehokkuus “kuolemaa vastaan”

Mukana tutkimuksessa on oireellisen COVIDin luvut, sairaalaan joutuminen, vakava sairaalahoito sekä näiden vastaavat tehokkuuslaskelmat. Taulukon alareunassa on tehokkuuslaskelmat kuoleman varalta. Me käytämme taulukkoa tekemään viimeisen tehokkuuslaskelman, jotta voisimme siirtyä puhumaan kammottavista misinformaation lähteistä.

Ikävuosien 16-44 välillä rokottamattomien ryhmässä mainitaan 36 kuolemaa ja 0 kuolemaa rokotettujen ryhmässä. Meillä on 88,938,310 ja 61,397,072 henkilöpäivää rokottamattomille ja rokotetuille vastaavasti taulukon alareunassa. Tästä saamme 100%:n tehokkuuden!

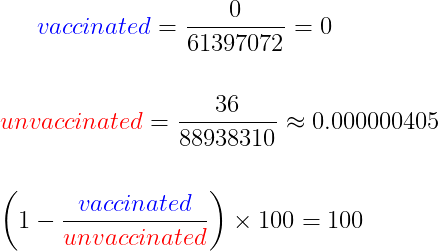
100% tehokkuus! Sataprosenttinen suoja kuolemaa vastaan! Ikäryhmät 16-44 eivät voi kuolla COVIDiin! Voit nähdä miten mahdotonta jollekin on kuolla rokotettuna, sillä he eivät edes kerro epävarmuudelle rajoja. 100 prosenttia ilman epävarmuutta on niin varma kuin vain voi olla.

Fataali erhe (vitsi tarkoituksella)

Selvästikin on mahdollista rokotetun 16-44 vuotiaan kuolla COVIDiin. Muut samanlaisen tehokkuuslaskelman tulokset ovat yhtä virheellisiä, ja niitä käytetään vaarallisen väärin. Piipahdetaan tri. Tomin, entisen CDC:n johtajan, luona.

It's actually pretty simple math. If you get Covid and you've been vaccinated, you're about 100 times less likely to die.

— Dr. Tom Frieden (@DrTomFrieden) July 27, 2021

Hypervalveilla olevat massarokotuksien puolestapuhujat ovat käyttäneet rokotteen tehokkuutta “kuolemaa” vastaan tässä israelilaisessa tutkimuksessa väittämään, että jos saat COVIDin sinulla on ylimääräinen suoja rokotteesta johtuen. Jotkut jopa lainaavat prosenttilukua (“se on 96% tehokas kuoleman ehkäisemisessä!”) niin ettei heitä syytettäisi lukujen päästä keksimisestä. Mutta jos olet päässyt tänne asti, olet tehnyt tehokkuuslaskelman jo kolme erillistä kertaa. Lasket asioita ja jaat laskettuja asioita.

Emme missään kohtaa, emme missään vaiheessa tarkastelleet sitä miten monta ihmistä rokotettujen ryhmässä oikeasti sai COVIDin ja kuoli. Me (ja tutkimuksen kirjoittajat) laskimme kuolemien lukumäärän rokotettujen joukossa ja jaoimme sen päivien määrällä, ei infektioiden määrällä.

Ja jos me tarkastelemme lukuja ja vertailemme kuolemia oikeasti infektion saaneiden joukossa, saamme aivan eri kuvan.

Tehokkuusluvut ovat misinformaatiota

Jokainen tehokkuusluku tähän päälle on redundantti. Kaikki raportoidut tulokset infektioista ovat seurausta vähentyneistä infektioista [4]. Tehokkuusluvut olisivat 9kymmenissä vaikka rokotettu ryhmä olisi täysin identtinen poislukien infektioaste.

Kun “CDC:n entinen johtaja” tri. Tom ja muut käyttävät ei-infektiotehokkuuslukuja puhumaan rokotteista, he, tarkoituksella tai ei, johtavat harhaan kansaa. Se on jotain minkä tulisi loppua välittömästi. Poislukien infektioaste, tehokkuusluvut eivät välitä mitään käyttökelpoista informaatiota kansalaisille niiden riskeistä sen jälkeen kun he ovat saaneet rokotteen. Sen sijaan, se voi aiheuttaa, että rokotettu asettaa itsensä suurempaan vaaraan mikäli hän toimii misinformaation pohjalta.

Tehokkuusluvut, kaikki muut paitsi infektioluvut, ovat kaikki seurausvaikutuksia infektiosta, ja niitä käytetään ja ne hyväksytään niinkuin ne olisivat lisänä COVID-infektion kerrosvaikutuksia.

Tämä kuvio näyttää miten ne kommunikoidaan ja miten ne vastaanotetaan kansan ja julkisuudenhenkilöiden piirissä. Jos olet rokotettu, se kommukoidaan niin, että tutkimus on näyttänyt että:

1. >90% vähemmän todennäköisesti saat tartunnan — totta
2. >90% vähemmän todennäköisesti saat oireita jos saat tartunnan — valetta
3. >90% vähemmän todennäköisesti joudut sairaalaan jos saat oireita — valetta
4. >90% vähemmän todennäköisesti joudut vakavaan sairaalahoitoon jos joudut sairaalaan — valetta
5. >90% vähemmän todennäköisesti kuolet jos joudut vakavaan sairaalahoitoon — valetta

Jos tehokkuusluvut olisivat lisäsuojaa antavia kerrannaistoimia, silloin havainnot olisivat olleet erilaisia israelilaisten tutkimuksessa (kaikki ikäluokat) [5].

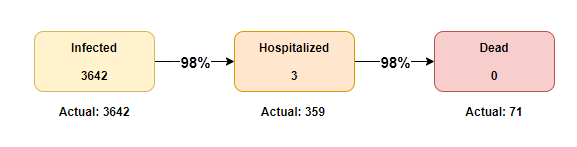
Näin pienillä luvuilla erot voivat tuntua mitättömiltä. Mutta kun ne skaalataan yli populaatioiden sekä yli ajan, vaikutus ihmisten päätöksentekoon heidän valitessaan minkä infektioriskitason olettaa voi muuttaa tilannetta dramaattisesti.

Tällä hetkellä melkein jokaikinen tekee näitä hyväksyttäviä katastrofisia virheitä. On vaikeaa käsittää sitä miten paljon enemmän väärässä sitä voi olla ja silti pysyä uskottavana tämän jälkeen. Mutta johtuen siitä, että nämä ovat hyväksyttäviä katastrofaalisia virheitä, jos minä onnistun hämmennyksen selventämisessä, misinformaation levittäjät yksinkertaisesti jatkavat eteenpäin seuraavaan hyväksyttävään katastrofaaliseen virheeseen.

Mitä luvut oikeasti kertoivat

Kun katsoo tarkemmin ikäryhmittäin sitä ketkä saivat tartunnan ja ketkä kuolivat, idea lisäsuojasta katoaa useimmilla.

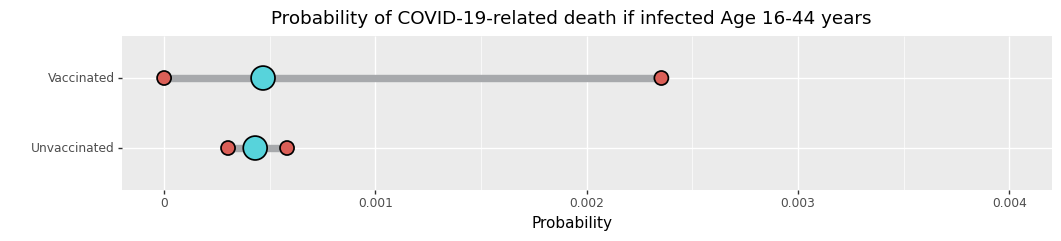
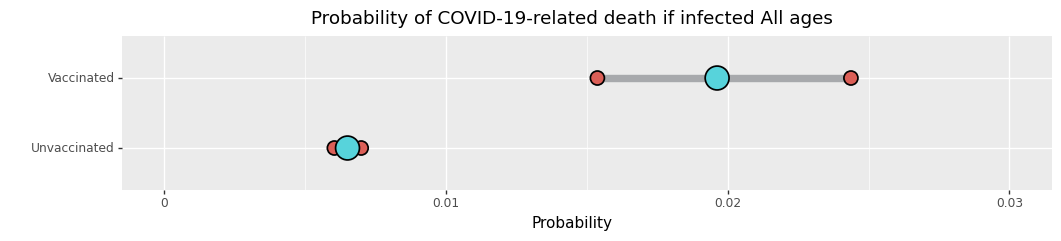
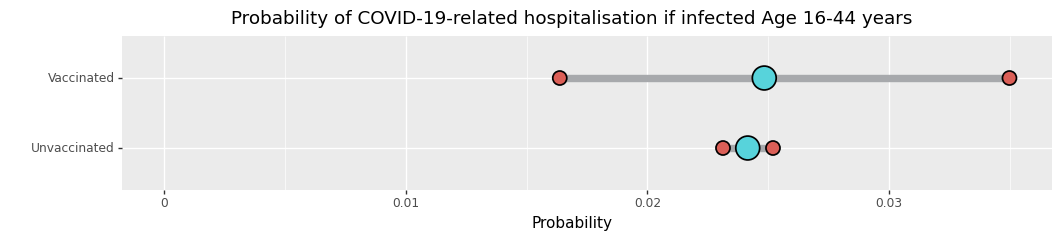
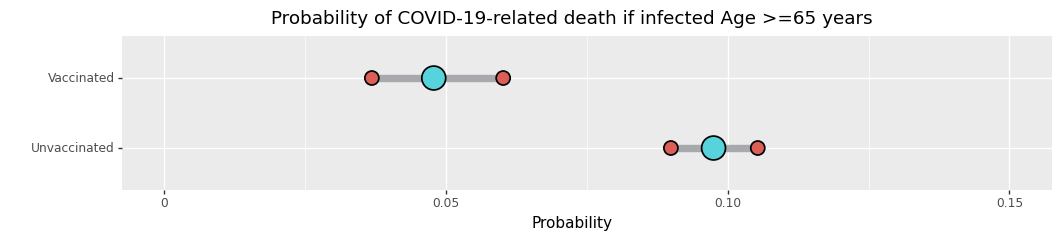
Kun lopultakin lasket asioita ja jaat lasketuilla asioilla sellaisia lukuja jotka oikeasti merkkaavat, kuten miten moni infektion saanut kuoli kussakin ryhmässä, 90%:n lukuja ei jää jäljelle. Ylläolevassa graafissa [6] ei näy informaatiota, jonka perusteella voitaisiin sanoa kuolleisuuden per infektio olevan eri rokotettujen ja rokottamattomien ryhmissä. Voit nähdä miksi tarkistamalla infektoitujen lukumäärän sekä kuolleiden lukumäärän kummassakin ryhmässä.

36 / 84611 rokottamattomien ryhmässä versus 0 / 1066 rokotettujen ryhmässä. 36 / 84611 on arviolta 1 / 2350, mutta meillä oli vain 1066 tartunnan saanutta rokotettujen ryhmässä. Ei ole tarpeeksi informaatiota väittää, että kuolleisuus per infektio olisi korkeampi tai matalampi, ja epävarmuus käy ilmi yllä esitetyssä graafissa. Se on ikuisuuksien mitan päässä suhteellisesta kuolemattomuudesta, jota tehokkuusluvulla 100% on viestitty.

Itse asiassa, jos rokotettujen ryhmässä olisi ollut 24 kuolemaa, raportoitu tehokkuus olisi ollu niinkin pieni kuin 3%! Koska tarkastelu koski alttiutta ajan funktiona, 24 kuolemaa olisi ollut samanlainen kuolleisuus ajan mittaan kuin 36 kuollutta rokottamattomien ryhmässä. Mutta selvästikin taudin saaneiden ryhmässä 36 kpl 84611:sta on paljon matalampi kuolleisuus kuin 24 kpl 1066:sta! Kuolleisuus ikäryhmissä 16-44 taudin saaneiden joukossa olisi pitänyt olla lähes 53 kertaa korkeampi että oltaisiin voitu raportoida, että rokote olisi ollut 3% tehokas kuoleman ehkäisijä.

Tarkastellaan paria muuta tilannetta.

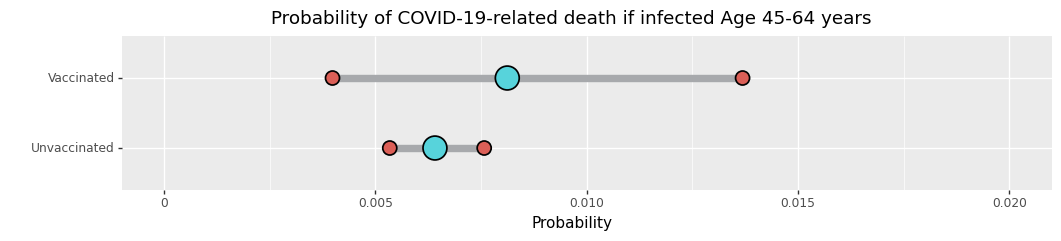
Ikäryhmille 45-64 ei ole tarpeeksi näyttöä todeta, että infektiot/tapauskuolleisuus olisi mitenkään eri, mutta kuten sininen viiva kertoo, numerot itse asiassa nojaavat kohti korkeampaa kuolleisuutta rokotettujen joukossa.

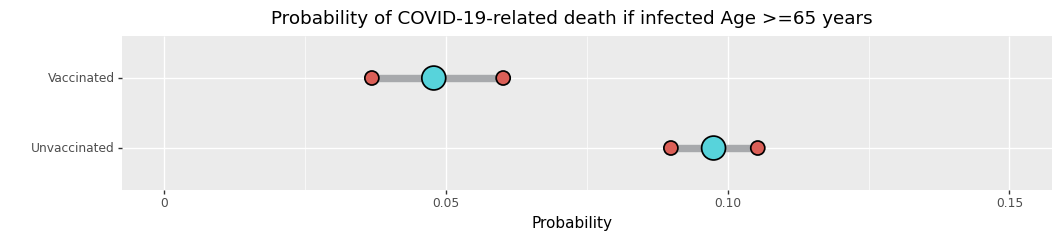
Hopeareunus tässä on, että 65-vuotiaiden ja vanhempien ryhmässä havaittu kuolleisuus kokeessa antaa meille hyvän syyn uskoa, että ehkäpä rokote voi vähentää kuolleisuutta tässä ryhmässä. Koska he olivat haavoittuvaisimpia alusta alkaen, tämä on lupaava tulos.

Post hoc ergo propter hoc

Jos huomaisit, että useat ihmiset ovat kuolleet rokotteen jälkeen, ja päättelisit että rokote on aiheuttanut kuoleman, tekisit niinkutsutun “post hoc ergo propter hoc” virheen.

Tämä on tarpeeksi yksinkertaisesti selitettävä päättelyvirhe. Vaikka B tapahtui A:n jälkeen, se ei tarkoita, että A on aiheuttanut B:n. Kausaation määrittäminen vaatii enemmän tietoa päättelyn tueksi.

Jos teit tämän virheen viestiessäsi rokotehuolista, todennäköisesti massarokotuksia ajavat huomauttaisivat nopeasti tästä päättelyvirheestä. Kuitenkin massarokotuksia ajavat tekevät tämän saman virheen ilman että heidän logiikkaansa haastetaan sen enempää omien joukosta.

Meillä on suuri syy esittää kausaalisuhde vähentyneiden tartuntamäärien ja rokotteen välillä. mRNA-rokotteet on suunniteltu niin, että niillä on kausaalimekanismi interaktiolle. Aiottujen kausaalimekanismin vaikutusten havainnointi makrotasolla (vähemmän infektioita) on kohtuullista liittää suunniteltuun mekanismiin mikrotasolla.

Meillä on paljon vähemmän syytä esittää kausaatiota infektion estämisen jatkopäätelmille. Massarokotuksia ajavat ovat käyttäneet heidän väärää ymmärrystä siitä miten tehokkuuslukuja on laskettu, ja sitten tehneet post hoc ergo propter hoc -argumentteja niillä. Jopa silloinkin kun data ei näytä minkäänlaista eroa, tehokkuuslukujen väärinymmärtäminen ja väärintulkinta automaattisesti pahenee post hoc ergo propter hoc -järkeilyllä. Nämä ovat valitettavasti hyväksyttäviä katastrofaalisia virheitä.

Tehokkuusmisinformaation vaarat

Minä tahansa päivänä sosiaalisesta mediasta on mahdollista löytää joku, joka on rokotettu ja joka sanoo saaneensa COVIDin, ja hän vain tietää että ilman rokotetta hän olisi ollut pahemmassa kunnossa. Nämä ilmoitukset saavat paljon huomiota. On ihanaa, että ihmiset ovat välttyneet pahimmilta oireilta, mutta data ei tue havaintoa siitä, että rokote tarjoaa merkittävää jälkihyötyä useimmille.

Tämän valheellisen idean toistaminen, että rokotteilla on huikeita ja merkittäviä lisähyötyjä pelkän vähentyneen infektioalttiuden lisäksi, johtaa siihen että ihmiset ottavat suurempia riskejä.

Henkilö, joka virheellisesti olettaa, että “rokotteen kanssa, vaikka saisin infektion, kuolen pienemmällä todennäköisyydellä kuin ilman rokotetta”, tulee todennäköisesti käyttäytymään tavoilla joilla hän saa todennäköisemmin infektion. Hän saattaa muuttua vain rokotettujen “se on vain flunssa”-totuudentorveksi.

Jos havaittu kerrosmainen suoja tehtäisiin selvemmäksi, silloin ihmiset saattaisivat edelleenkin pitää maskeja ja etäisyyttä, mikä edelleen pienentää heidän altistumistaan rokotteen lisäksi. He saattavat mennä vähemmän sosiaalisiin tapahtumiin. Tämä taas pienentäisi infektioastetta edelleen, ja vähentäisi todennäköisyyttä sille, että mutaatio pääsee läpi rokotteesta. (Tätä artikkelia kirjoitettaessa Valkoinen talo oli muuttanut maskisuositustaan rokotetuille)

Ne, jotka vahvasti uskovat että kaikkien tulisi ottaa rokote, voivat valita edelleen promota tehokkuuslukuja lisäsuojana, koska heidän tavoitteensa on rohkaista ihmisiä ottamaan rokote. Numeroiden harhaanjohtava käyttö mainosnumeroina on yhtä vanha temppu kuin aika itse. Mutta he tekevät sen sekä heidän rehellisyytensä että uskottavuutensa hinnalla, ja he uhraavat osan niistä oikeista hyödyistä joita rokotteet saattaisivat tarjota, antamalla ihmisille epätarkkaa informaatiota jonka pohjalta tehdä valintoja.

Henkilökohtaiset todennäköisyydet vs alttiudet ajan mittaan

Ne, jotka tykkäävät sanoa “numerot puhukoon puolestaan” ovat kaikkein vähiten todennäköisiä ymmärtämään sitä mitä numerot sanovat. Tutkimukset tekevät epidemiologisia oletuksia ja raportoivat eri yleisöille kuin ne kenelle numeroita näytetään. Siinä missä voi olla joitain tutkimuksia, joissa nämä luvut on laskettu ehdollisesti, ne ovat epäyhteensopivia niiden kanssa joissa luvut on laskettu ehdottomasti. Tämä informaatio ei ole todennäköisesti mukana lukujen yhteydessä, ja niitä tullaan käyttämään toistensa tilalla samoin tavoin.

Väärä yleisö

Sairaala, joka pyrkii suunnittelemaan resurssienkäyttöä ja työvoimaansa, on kiinnostunut arvioiduista päivittäisistä sairaalatapauksista ja kuolleisuusluvuista, kun otetaan huomioon se miten monta ihmistä on saanut rokotteen. Poliittinen päättäjä päättämässä niistä toimista joilla taistella koronavirusta vastaan välittää siitä mitkä ovat päivittäiset luvut eri metriikoille sen jälkeen, kun jokin toimi on otettu käyttöön.

Henkilö, useimmassa tapauksessa, ei kiinnostu päivittäisistä populaatiotason luvuista. Häntä kiinnostaa omat todennäköisyytensä tai hänen rakkaimpien todennäköisyydet.

Tavalliselle tallaajalle ei ole väliä sillä jos päivittäin havaittu infektioaste on matala kaikilla, jos he itse ovat merkittävästi korkeammassa riskissä. Kuitenkin, koska ei ole keinoja jotka voivat ohjata yksilöä arvioimaan omia riskejään, raportti päivittäisestä infektioasteesta rokotettujen ja rokottamattomien välillä antaa jotain käyttökelpoista mittaria, kun puhutaan rokottautumispäätöksestä.

Mutta kun henkilö on ottanut rokotteen, päivittäinen sairaalatapausten määrä, päivittäinen kuolemien määrä ei ole enää merkityksellinen. Paitsi aivan äärimmäisessä tapauksessa, kuten silloin kun resurssit on loppu, päivittäisellä kuolemien lukumäärällä on suhde henkilön todennäköisyyteen kuolla tartunnan saadessa. Henkiön tarvitsee tietää omat todennäköisyytensä mikäli hän lopulta saisi tartunnan.

Tuhoon tuomittu tilanne

Tämän artikkelin alussa kiusoittelin, että data näyttää rokotettujen tartunnan saaneiden kuolleisuuden olevan korkeampi kuin rokotttamattomien tartunnan saaneiden. Tämä on totta kuolemantapauksissa ja myöskin totta sairaalatapauksissa.

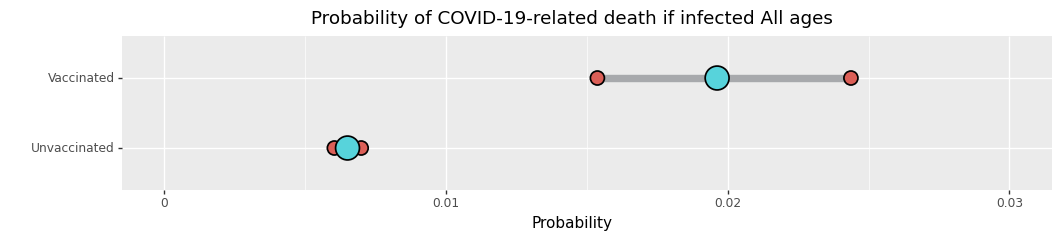
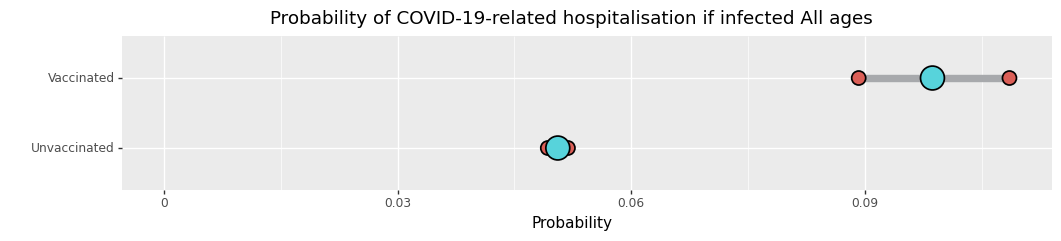
Tässä ei ole mitään vilunkipeliä. Nämä tulokset ovat päivänselviä Israelin sdatassa mikäli joku olisi vaivautunut vaan niitä tarkastelmaan. Se on seurausta asioiden laskemisesta ja laskettujen asioiden jakamisesta, joista ihmiset oikeasti halusivat saada tietoa. Ei ainoastaan tuo, vaan myös se että tulokset ovat epäloogisia, ja nyt helpommin ennustettavissa. Ne myös tapahtuvat kaikkialla muualla ja aiheuttavat hämmennystä.

Miksi kuolleisuusluvut ovat korkeammat?

Syy on piilotettu, se on että suuri määrä ihmisiä, jotka eivät koskaan olleet kuolemassa, eivät enää saa tartuntaa.

Maanisesti misinformaatiota levittämällä siitä, että ihmisillä olisi jotain ylimääräistä hyötyä rokotuksesta kuolemaa vastaan jos he saisivat tartunnan, kun rohkaistaan kaikkia ottamaan rokote, käy selväksi tuntematon fakta siitä, että ne jotka kaikkein todennäköisimmin kuolevat (6.6 per 100,000) [7] ovat nyt niitä jotka kaikkein todennäköisimmin saavat tartunnan (2.5 per 100,000).

Vertaa tätä niihin, jotka olivat vähiten todennäköisimmin kuolemassa (0.04 per 100,000), he ovat nyt niitä jotka vähiten todennäköisimmin saavat tartunnan (1.7 per 100,000).

Nämä tulokset ovat samankaltaisia ympäri maailman. Britanniassa, joka seuraa eri variantteja, raportoidaan että deltavarianttitapauksissa kahdesti rokotetut kuolivat tahdilla 0.0078 per infektio ja rokottamattomat kuolevat tahdilla 0.0014 per infektio. Kuolleisuus per infektio oli 5.6-kertainen rokotetuilla.

Ilman huolellista kontrollia ja ymmärrystä saattaisi virheellisesti tehdä päätelmän, että deltavariantti on tappavampi mikäli on saanut rokotteen, että rokote on menettämässä tehoaan, että rokote tekee ihmisistä heikompia, tai jokin näiden kombinaatio. Vaikka kaikki noista lopputulemista tässä ympäristössä ovat mahdollisia, jos emme ole tietoisia infektion aiheuttaman kuolleisuuden ongelmasta heti alusta alkaen, koska on niin kiire levittää misinformaatiota ylimääräisistä suojatasoista joita data ei tue, saattaa mennä ohi se miten oikeasti kontrolloida näitä ylimääräisiä vaikutuksia ja analysoida uutta dataa kun sitä saadaan.

Kuolleisuus infektiotapauksessa tulee aina olemaan suurempi rokotettujen ryhmässä jos suurin osa rokotetuista on niitä, jotka ovat todennäköisesti kuolemassa huolimatta siitä onko rokotuksen ottanut vaiko ei.

Nuo pirun hyväksyttävät katastrofaaliset virheet

Jotkut ihmiset saattavat yksinkertaisesti nostaa kätensä ilmaan kun heille tästä ongelmasta kertoo. Jotkut, jotka ymmärtävät että kausaalitasolla tehokkuusmittarit olivat mittareita ajan funktiona, eivät välttämättä ymmärrä sitä mikä on ongelma kun käytetään aikamittareita rokotteiden mainostukseen. Jossain määrin rokotteet muuttavat todennäköisyyttä kun joku sellaisen ottanut kuolee COVIDiin.

Onko se oikeasti niin iso juttu, että tunnusluvut ovat kaikki tuplasti, triplasti ja nelinkertaisesti laskeneet infektioita niistä johtuviksi hyödyiksi omiin vähentyneisiin infektiolukuihinsa? Onko se oikeasti ongelma, jos sanoo jollekulle että hän kuolee 100 kertaa todennäköisemmin jos hän saa COVIDin ja on rokotettu, mikäli se vakuuttaa hänet ottamaan rokotteen?

Kyllä se on.

Viitteet

[1] Alkuvaiheen suuren mittaluokan tutkimus Israelista näyttää arviolta 3-kertaisen, uusi data Britanniasta näyttää arviolta 5.6-kertaisen kuolleisuusasteen rokotetuilla.

[2] Mitä 95% tehokkuus COVID-rokotteilla oikeasti tarkoittaa? – The Lancet, March 8, 2021

[3] Nämä kirjoittajat mainitsevat negatiivisen binomiregression käytön Stata-ohjelmistolla, jolla laskea luottamusvälejä, ja se on mahdollista että heidän piste-estimaattinsa on myös tämän regression sivutuote. Ilman pääsyä tiedostoihin joilla ajaa regressio uudelleen, tällä hetkellä ei ole mahdollista sanoa onko kyseessä virhe vaiko regressio joka on tämän eron syynä.

[4] Tämä voidaan osoittaa monin eri tavoin. Todennäköisyyden teoriaa tunteville, jos E_n on mikä tahansa valittu rokotteenjälkeinen tapahtuma ja E_1 on infektio,

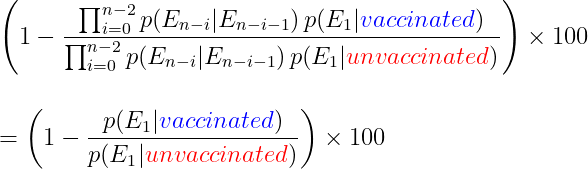
Ilman merkittävää työtä, jolla selvitellä rokotteenjälkeisiä vaikutuksia, muut tehokkuusluvut kuin infektio tulevat toistelemaan infektion tehokkuutta.

[5] Oletetaan aluksi, että sairaalatapaus/infektioaste on sama kuin rokottamattomilla, sitten sovelletaan 98% suojaa päälle. (5556/109876)*0.02 = 3.7

[6] Betaposteriorijakauma Jeffreysin priorilla. 95%:n luottamusväli

[7] Näyttö joka on olemassa tässä datassa 65-vuotiaiden ja sitä vanhempien rokotettujen vähentyneestä kuolleisuudesta 50%:n kohdalle pienentää heidän kuolleisuuttaan lukuun arviolta 3.3 per 100,000. Tämä on hyvä, mutta silti paljon suurempi kuin muilla ryhmillä ja tarpeeksi suuri vaikuttaakseen lopputulokseen.

Artikkelin julkaissut drrollergator.substack.com